题目内容
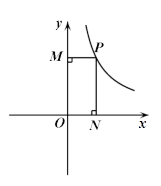
如图,P是反比例函数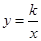 (
(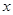 >0)的图象上的一点,PN垂直
>0)的图象上的一点,PN垂直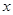 轴于点N,PM
轴于点N,PM
垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数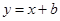 的图象经过点P.
的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线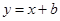 与
与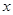 轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的
轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的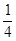 时,直接写出点Q的坐标.
时,直接写出点Q的坐标.
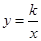 (
(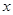 >0)的图象上的一点,PN垂直
>0)的图象上的一点,PN垂直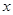 轴于点N,PM
轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数
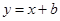 的图象经过点P.
的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线
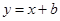 与
与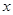 轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的
轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的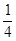 时,直接写出点Q的坐标.
时,直接写出点Q的坐标.解:(1)∵PN垂直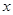 轴于点N,PM垂直y轴于点M,矩形
轴于点N,PM垂直y轴于点M,矩形
OMPN的面积为2 ,且ON=1,
∴PN=2.
∴点P的坐标为(1,2).…………………1分
∵反比例函数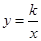 (
(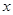 >0)的图象、一次函数
>0)的图象、一次函数
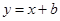 的图象都经过点P,
的图象都经过点P,
由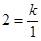 ,
,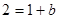 得
得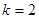 ,
,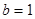 .
.
∴反比例函数为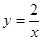 ,……………………………2分
,……………………………2分
一次函数为 . ……………………………………3分
. ……………………………………3分
(2)Q1(0,1),Q2(0,-1). ……………………………5分
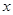 轴于点N,PM垂直y轴于点M,矩形
轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2 ,且ON=1,
∴PN=2.
∴点P的坐标为(1,2).…………………1分
∵反比例函数
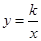 (
(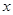 >0)的图象、一次函数
>0)的图象、一次函数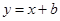 的图象都经过点P,
的图象都经过点P,由
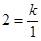 ,
,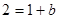 得
得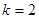 ,
,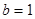 .
.∴反比例函数为
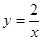 ,……………………………2分
,……………………………2分一次函数为
 . ……………………………………3分
. ……………………………………3分(2)Q1(0,1),Q2(0,-1). ……………………………5分
(1)利用矩形的面积求出P点坐标,从而求出反比例函数和一次函数的解析式,
(2)一次函数x轴的交点为(-1,0),点Q在y轴,所以△QOA的面积= OA
OA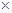 OQ=
OQ=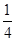 ,即可求得OQ的值
,即可求得OQ的值
(2)一次函数x轴的交点为(-1,0),点Q在y轴,所以△QOA的面积=
 OA
OA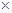 OQ=
OQ=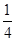 ,即可求得OQ的值
,即可求得OQ的值
练习册系列答案
相关题目
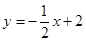 与
与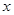 轴交于
轴交于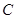 ,与
,与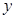 轴交于
轴交于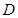 ,以
,以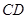 为边作矩形
为边作矩形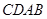 ,点
,点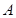 在
在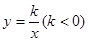 经过点
经过点 与直线
与直线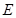 ,
,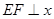 轴于
轴于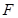 ,则
,则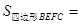 .
.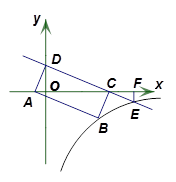
 (x>0)的图像经过A、E两点,若□AOBC的面积为9,则k= ▲ .
(x>0)的图像经过A、E两点,若□AOBC的面积为9,则k= ▲ .
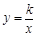 的图象上一点,PA⊥x轴于点A,
的图象上一点,PA⊥x轴于点A,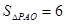 ,则k = ________.
,则k = ________. 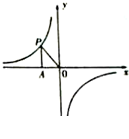
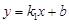 的图象与反比例函数
的图象与反比例函数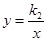
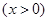 的图象交于
的图象交于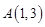 ,
,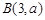 两点.
两点.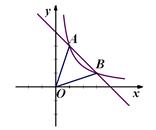
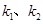 的值;
的值;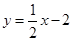 的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数
的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数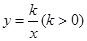 的图象于Q,
的图象于Q,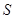 △OCQ=
△OCQ=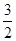
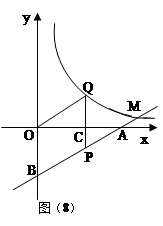
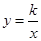 图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=
图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=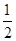 ,则T1·T2·…·T2012=【 】
,则T1·T2·…·T2012=【 】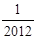
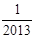
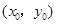 在函数
在函数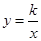 (x<0)的图象上,且
(x<0)的图象上,且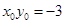 ,则它的图象大致是( )
,则它的图象大致是( )