题目内容

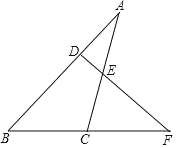
【题目】已知：如图△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=2cm.则CB的长=( )．

A. 8cm B. 6cm C. 4cm D. 2cm

【答案】B

【解析】

根据三角形内角和定理和等腰三角形性质求出∠B、∠BAC度数，再求得∠DAC=∠C，根据等腰三角形的性质可得AD=DC=2cm，，根据含30度角的直角三角形性质求出BD=2AD=4cm，由BC=BD+CD即可求解．

∵AB=AC，∠C=30°，

∴∠B=∠C=30°，∠BAC=180°-30°-30°=120°，

∵AB⊥AD，

∴∠BAD=90°，

∴∠DAC=120°-90°=30°=∠C，

∴AD=DC=2cm，

∵∠BAD=90°，∠B=30°，AD=2cm，

∴BD=2AD=4cm，

∴BC=4cm+2cm=6cm．

故选B.

练习册系列答案
相关题目

【题目】课堂上学习了勾股定理后，知道“勾三、股四、弦五”．王老师给出一组数让学生观察：3、4、5；5、12、13；7、24、25；9、40、41；…，学生发现这些勾股 数的勾都是奇数，且从 3 起就没有间断过，于是王老师提出以下问题让学生解决．

(1)请你根据上述的规律写出下一组勾股数：11、________、________；

(2)若第一个数用字母a(a为奇数，且a≥3)表示，那么后两个数用含a的代数式分别怎么表示？小明发现每组第二个数有这样的规律4=，12=，24=……，于是他很快表示了第二数为 ，则用含a的代数式表示第三个数为________；

(3)用所学知识证明你的结论．

【题目】（1）已知一个多边形的内角和是它的外角和的 3 倍，求这个多边形的边数．

（2）如图，点F 是△ABC 的边 BC 延长线上一点．DF⊥AB，∠A=30°，∠F=40°，求∠ACF 的度数．

【题目】如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．

（1）求证：BG＝CF．

（2）请你判断BE+CF与EF的大小关系，并说明理由．

【题目】如图，已知△ABC 中，AB=AC=6cm，∠B=∠C，BC=4cm，点 D 为 AB的中点．

（1）如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动，同时，点 Q 在线段 CA 上由点 C 向点 A 运动．

①若点 Q 的运动速度与点 P 的运动速度相等，经过 1 秒后，△BPD 与△CQP 是否全等，请说明理由；

②若点 Q 的运动速度与点 P 的运动速度不相等，当点 Q 的运动速度为多少时，能够使△BPD 与△CQP 全等？

（2）若点 Q 以②中的运动速度从点 C 出发，点 P 以原来的运动速度从点 B 同时出发，都逆时针沿△ABC 三边运动，则经过 后，点 P 与点 Q 第一次在△ABC 的 边上相遇？（在横线上直接写出答案，不必书写解题过程）

【题目】某农户种植一种经济作物，总用水量y(m3)与种植时间x(天)之间的函数关系如图所示．

(1)第20天的总用水量为 m3；

(2)当x≥20时，求y与x之间的函数表达式；

(3)种植时间为多少天时，总用水量达到7 000 m3.

【题目】如图，在Rt△ABC中，∠C=30°，以直角顶点A为圆心，AB长为半径画弧交BC于点D，过D作DE⊥AC于点E．若DE=a，则△ABC的周长用含a的代数式表示为 ．

【题目】如图，线段AB的两个端点坐标分别为A（1，1），B（2，1），以原点O为位似中心，将线段AB放大后得到线段CD.若CD=2，则端点C的坐标为（　　）
A.（2，2）
B.（2，4）
C.（3，2）
D.（4，2）

【题目】满足下列条件的△ABC ， 不是直角三角形的是（　　）
A.∠C=∠A+∠B
B.a：b：c=3：4：5
C.∠C=∠A-∠B
D.∠A：∠B：∠C=3：4：5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网