题目内容
【题目】如图,平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.
(1)求菱形ABCD的边长;
(2)求双曲线的解析式.

【答案】(1)5;(2)![]() .
.
【解析】试题分析:![]() 过点C作CE⊥AB于点E,设菱形的边长为
过点C作CE⊥AB于点E,设菱形的边长为![]() ,则
,则![]()
![]() 在
在![]() 中,利用勾股定理建立关于
中,利用勾股定理建立关于![]() 的方程,解方程求出
的方程,解方程求出![]() 的值即可.
的值即可.
![]() 设双曲线的解析式为
设双曲线的解析式为![]() ,过点D作DF⊥AB于点F,分别求出
,过点D作DF⊥AB于点F,分别求出![]() 的长,则点D的坐标可知,代入双曲线的解析式求出
的长,则点D的坐标可知,代入双曲线的解析式求出![]() 的值即可.
的值即可.
试题解析:(1)设菱形的边长为x,则BC=AB=x.
如图,过点C作CE⊥AB于点E.
∵点A的坐标为(2,0),点C的坐标为(10,4),
∴OA=2,CE=4,OE=10,
∴BE=OE-OA-AB=10-2-x.
在Rt△BEC中,由勾股定理可得BC2=BE2+CE2,
即x2=(10-2-x)2+42,
解得x=5,
∴菱形ABCD的边长为5.
(2)设双曲线的解析式![]() .如图,过点D作DF⊥AB于点F,
.如图,过点D作DF⊥AB于点F,
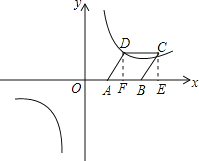
则DF=CE=4,EF=CD=5,
∴OF=OE-EF=10-5=5,
∴点D的坐标为(5,4),
∴k=20,
∴双曲线的解析式为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

