题目内容
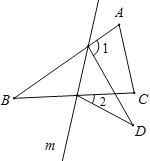
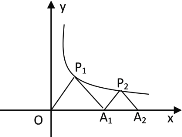
【题目】如图,![]() 与
与![]() 是两个全等的等边三角形,
是两个全等的等边三角形,![]() .有下列四个结论:①
.有下列四个结论:①![]() ;②
;②![]() ;③直线
;③直线![]() 垂直平分线段
垂直平分线段![]() ;④四边形
;④四边形![]() 是轴对称图形.其中正确的结论有_____.(把正确结论的序号填在横线上)
是轴对称图形.其中正确的结论有_____.(把正确结论的序号填在横线上)
【答案】②③④
【解析】
①通过全等和等边三角形的性质解出答案即可判断;②根据题意推出即可判断;③延长BM交CD于N,利用外角定理推出即可判断;④只需证明四边形ABCD是等腰梯形即可判断.
①∵△ABM≌△CDM,△ABM、△CDM都是等边三角形,
∴∠ABM=∠AMB=∠BAM=∠CMD=∠CDM=∠DCM=60°,AB=BM=AM=CD=CM=DM,
又∵MA⊥MD,
∴∠AMD=90°,
∴∠BMC=360°﹣60°﹣60°﹣90°=150°,
又∵BM=CM,
∴∠MBC=∠MCB=15°;
②∵AM⊥DM,
∴∠AMD=90°,
又∵AM=DM,
∴∠MDA=∠MAD=45°,
∴∠ADC=45°+60°=105°,
∠ABC=60°+15°=75°,
∴∠ADC+∠ABC=180°;
③延长BM交CD于N,
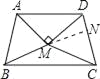
∵∠NMC是△MBC的外角,
∴∠NMC=15°+15°=30°,
∴BM所在的直线是△CDM的角平分线,
又∵CM=DM,
∴BM所在的直线垂直平分CD;
④根据②同理可求∠DAB=105°,∠BCD=75°,
∴∠DAB+∠ABC=180°,
∴AD∥BC,
又∵AB=CD,
∴四边形ABCD是等腰梯形,
∴四边形ABCD是轴对称图形.
故答案为:②③④.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目