题目内容
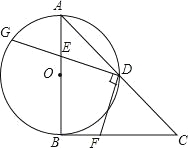
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.

【答案】(1) 详见解析;(2)![]() .
.
【解析】
试题分析:(1) 连接OC,由已知条件易得∠CAD=∠OCA,∠OCA=∠OAC,所以∠CAD=∠CAO,即可得AC平分∠DAB;(2).连接BE交OC于点H,易证OC⊥BE,可知∠OCA=∠CAD,因COS∠HCF=![]() ,可设HC=4,FC=5,则FH=3.由△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,所以OH=2x ,在△OBH中,由勾股定理列方程求解即可.
,可设HC=4,FC=5,则FH=3.由△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,所以OH=2x ,在△OBH中,由勾股定理列方程求解即可.
试题解析:(1)证明:连接OC,则OC⊥CD,
又AD⊥CD,
∴AD∥OC,
∴∠CAD=∠OCA,
又OA=OC,∴∠OCA=∠OAC,
∴∠CAD=∠CAO,
∴AC平分∠DAB.
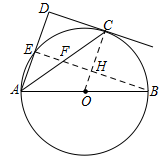
(2)解:连接BE交OC于点H,易证OC⊥BE,可知∠OCA=∠CAD,
∴COS∠HCF=![]() ,设HC=4,FC=5,则FH=3.
,设HC=4,FC=5,则FH=3.
又△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,∴OH=2x
∴BH=HE=3x+3 OB=OC=2x+4
在△OBH中,(2x)2+(3x+3)2=(2x+4)2
化简得:9x2+2x-7=0,解得:x=![]() (另一负值舍去).
(另一负值舍去).
∴![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
【题目】某校九年级(1)班全体学生2018年初中毕业体育考试的成绩统计如表:
成绩(分) | 20 | 22 | 24 | 26 | 28 | 30 |
人数(人) | 1 | 5 | 4 | 10 | 15 | 10 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有45名同学
B. 该班学生这次考试成绩的众数是28
C. 该班学生这次考试成绩的平均数是25
D. 该班学生这次考试成绩的中位数是28