题目内容
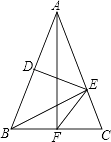
【题目】如图,Rt△ABC中,∠ACB=90°,CA=CB=2,CD⊥AB于D,点P是线段CD上的一个动点,以点P为直角顶点向下作等腰直角△PBE,
连接DE ,则DE的最小值为__________.

【答案】1
【解析】连接AE,先证明∠BAE的度数为定值,即∠BAE=∠BCP=45°,再根据垂线段最短,当DE⊥AE时,DE最小,此时三角形ADE是等腰直角三角形,解直角三角形可得.
∵△ABC和△EBP均为等腰直角三角形
∴△ABC∽△EBP,且∠ABC=∠EBP=45°
∴![]() ,且∠CBP=∠ABE
,且∠CBP=∠ABE
∴△CBP∽△ABE
∴∠BCP=∠BAE
∵CA=CB,∠ACB=90°,CD⊥AB
∴∠BCP=45°
∴∠BAE=∠BCP=45°
即∠BAE的度数为定值,
当DE⊥AE时,DE最小,此时三角形ADE是等腰直角三角形,
因为,三角形ABC是等腰直角三角形,CA=CB=2,CD⊥AB
所以,AD=![]()
所以,设AE=DE=x,则由AE2+DE2=AD2得,2x2=2,
解得x=1
所以,DE=1.
故答案为:1

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目