Question

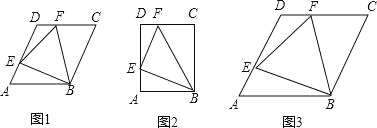
【题目】在ABCD中，AB＝6，AD＝8，∠B是锐角，将△ACD沿对角线AC所在直线折叠，点D落在△ABC所在平面内的点E处．如果AE恰好经过BC的中点，那么ABCD的面积是________．

Answer 1

【答案】12

【解析】如图，设AE、BC的交点为O，在△ABC与△CDA中，AB=CD，BC=DA，AC=CA，可得△ABC≌△CDA，由折叠可得△CDA≌△CEA，根据全等三角形的性质即可得∠ACB=∠CAE，BC=EA，在△AOC中，由于∠ACB=∠CAE，则有AO=CO，所以OB=OE，因O也是AE的中点，所以AO=CO=OB=OE．即可得四边形ABEC是矩形，ABCD的面积是就是长方形的面积，在Rt△AEC中，AC=6，AE=AD=8，由勾股定理得求得EC= ，所以ABCD的面积=ACCE=6×=．