题目内容
【题目】如图1,在ABCD中,E、F两点分别从A、D两点出发,以相同的速度在AD、DC边上匀速运动(E、F两点不与ABCD的顶点重合),连结BE、BF、EF.
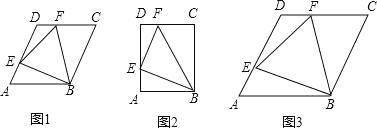
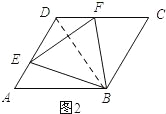
(1)如图2,当ABCD是矩形,AB=6,AD=8,∠BEF=90°时,求AE的长.
(2)如图2,当ABCD是菱形,且∠DAB=60°时,试判断△BEF的形状,并说明理由;
(3)如图3,在第(2)题的条件下,设菱形ABCD的边长为a,AE的长为x,试求△BEF面积y与x的函数关系式,并求出y的最小值.
【答案】(1)2;(2)等边三角形;(3)![]()
【解析】
试题分析:(1)依据矩形的性质可知∠D=∠A=90°,接下来,依据同角的余角相等可得到∠DFE=∠AEB,然后依据ASAS证明△DEF≌△ABE,依据全等三角形的性质可得到DE=6,从而可求得AE的长;
(2)连结BD.首先证明△ADB为等边三角形,于是得到BD=BC,然后再证明△BED≌△BFC,△AEB≌△DFB,由全等三角形的性质得到BE=BF,∠ABE=∠DBF,接下来证明∠EBF=60°,从而可判定△EBF为等边三角形.
(3)过点E作EM⊥AB,EN⊥DC,垂足为M、N,过点B作BG⊥DC,垂足为G.首先依据特殊锐角三角函数值可求得EM=![]() x,NE=
x,NE=![]() (a﹣x),BG=
(a﹣x),BG=![]() a,然后依据△EFB的面积=菱形的面积﹣△AEB的面积﹣△DFE的面积﹣△FCB的面积列出y与x的函数关系式,最后依据二次函数的性质求解即可.
a,然后依据△EFB的面积=菱形的面积﹣△AEB的面积﹣△DFE的面积﹣△FCB的面积列出y与x的函数关系式,最后依据二次函数的性质求解即可.
试题解析:(1)如图1所示:
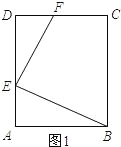
∵四边形ABCD为矩形,
∴∠D=∠A=90°.
∵∠BEF=90°,
∴∠DEF+∠AEB=90°.
又∵∠DEF+∠DFE=90°,
∴∠DFE=∠AEB.
在△DEF和△ABE中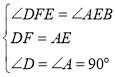 ,
,
∴△DEF≌△ABE.
∴AB=DE=6.
∴AE=AD﹣DE=8﹣6=2.
(2)如图2所示:连结BD.
∵四边形ABCD为菱形,∠A=60°,
∴AD=AB=DC=BC,∠EDB=60°.
∵∠A=60°,AD=AB,
∴△ADB为等边三角形.
∴AD=AB=BD.
∴DB=BC.
∵AD=DC,AE=DF,
∴DE=FC.
在△BED和△BFC中,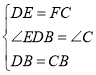 ,
,
∴△BED≌△BFC.
∴BE=BF.
在△AEB和△DFB中 ,
,
∴△AEB≌△DFB.
∴∠ABE=∠DBF.
∴∠EBF=∠EBD+∠DBF=∠ABE+∠EBD=60°.
∴△EBF为等边三角形.
(3)如图3所示:过点E作EM⊥AB,EN⊥DC,垂足为M、N,过点B作BG⊥DC,垂足为G.
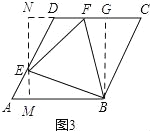
∵AE=DF=x,
∴DE=FC=a﹣x.
∵∠A=∠NDE=∠C=60°,
∴EM=![]() x,NE=
x,NE=![]() (a﹣x),BG=
(a﹣x),BG=![]() a.
a.
∵△EFB的面积=菱形的面积﹣△AEB的面积﹣△DFE的面积﹣△FCB的面积,
∴y=![]() a·a﹣
a·a﹣![]() a·
a·![]() x﹣
x﹣![]() ·x·
·x·![]() (a﹣x)﹣
(a﹣x)﹣![]() ·(a﹣x)·
·(a﹣x)·![]() a.
a.
∴y=![]() x2﹣
x2﹣![]() ax+
ax+![]() a2.
a2.
∴当x=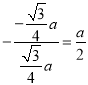 时,y取得最小值为
时,y取得最小值为![]() .
.