题目内容
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点. 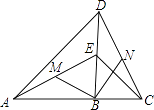
(1)求证:△ABE≌△DBC;
(2)判定△BMN的形状,并证明你的结论.
【答案】
(1)解:在△ABE和△DBC中 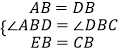 ,
,
∴△ABE≌△DBC
(2)解:△MBN是等腰直角三角形.
证明如下:
∵△ABE≌△DBC,
∴AE=CD,∠BAM=∠BDN.
∵M,N分别是AE,CD的中点,
∴AM= ![]() AE,CN=
AE,CN= ![]() CD.
CD.
∴AM=CN.
在△ABM和△DBN中 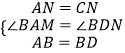 ,
,
∴ABM≌△DBN.
∴BM=BN,∠ABM=∠DBN.
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠ABM+∠DBM=90°.
∴∠DBN+∠DBM=∠MBN=90°.
∴△MBN是等腰直角三角形.
【解析】(1)在△ABE和△DBC中依据SAS可证明△ABE≌△DBC;(2)依据全等三角形的性质可得到AE=CD,∠BAM=∠BDN,然后依据中点的定义可证明AM=CN,依据SAS可证明ABM≌△DBN,然后全等三角形的性质可得到BM=BN,∠ABM=∠DBN,最后由∠ABM+∠MBE=∠MBE+∠EBN=90°可得到问题的答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
