题目内容
【题目】如图，直线
与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（ ）
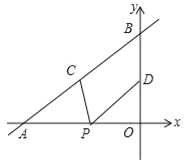
A．（﹣3，0） B．（﹣6，0） C．（
，0） D．（
，0）
【答案】C．
【解析】
试题分析：作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图所示．
令
中x=0，则y=4，∴点B的坐标为（0，4）；
令中y=0，则
，解得：x=﹣6，∴点A的坐标为（﹣6，0）．
∵点C、D分别为线段AB、OB的中点，∴点C（﹣3，2），点D（0，2）．
∵点D′和点D关于x轴对称，∴点D′的坐标为（0，﹣2）．
设直线CD′的解析式为y=kx+b，∵直线CD′过点C（﹣3，2），D′（0，﹣2），∴有
，解得：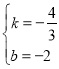
，∴直线CD′的解析式为
．
令中y=0，则
，解得：x=
，∴点P的坐标为（，0）．
故选C．
练习册系列答案
相关题目
【题目】目前节能灯在各城市已基本普及，今年某市面向县级及农村地区推广，为响应号召，朝阳灯饰商场用了4200元购进甲型和乙型两种节能灯．这两种型号节能灯的进价、售价如表：
进价（元/只） | 售价（元/只） | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
特别说明：毛利润=售价﹣进价
（1）朝阳灯饰商场销售甲型节能灯一只毛利润是元；
（2）朝阳灯饰商场购买甲，乙两种节能灯共100只，其中买了甲型节能灯多少只？
（3）现在朝阳灯饰商场购进甲型节能灯m只，销售完节能灯时所获的毛利润为1080元．求m的值.
