��Ŀ����
����Ŀ����ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ�����a��b��Ϊ��������a��b������ͼ�������ü������ȷֳ��Ŀ���ͬС�����Σ�Ȼ��ͼ2��ʽƴ��һ���������Σ�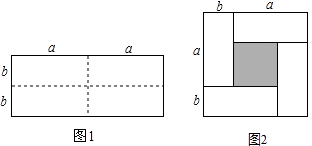
��1������Ϊͼ2�д������εı߳�Ϊ��С�����Σ���Ӱ���֣��ı߳�Ϊ �� ���ú�a��b�Ĵ���ʽ��ʾ��
��2����ϸ�۲�ͼ2������д��������������ʽ����a��b��2 �� ��a+b��2 �� ab����ʾ��ͼ�����֮�����ȹ�ϵ����ѡȡ�ʺ�a��b����ֵ������֤��
��3����֪a+b=4��ab=3�������ʽa��b��ֵ��
���𰸡�
��1��a+b,a��b
��2���⣺��a+b��2=��a��b��2+4ab��
���磺��a=5��b=2ʱ��
��a+b��2=��5+2��2=49
��a��b��2=��5��2��2=9
4ab=4��5��2=40
��Ϊ49=40+9��
���ԣ�a+b��2=��a��b��2+4ab
��3���⣺��a+b=4��
��a+b��2=16��
�ߣ�a+b��2=��a��b��2+4ab��ab=3��
�ࣨa��b��2=��a+b��2��4ab=16��4��3=4��
��a��b=2��a��b=��2��
��a��b��
��a��b=2
���������⣺��1����������ã�
�������εı߳�Ϊa+b��
С�����Σ���Ӱ���֣��ı߳�Ϊa��b��
�ʴ�Ϊ��a+b��a��b��
��1����������õ��������εı߳�Ϊa+b��С�����Σ���Ӱ���֣��ı߳�Ϊa��b����2������ͼ�ε�����õ���a+b��2=��a��b��2+4ab����3����a+b=4���õ���a+b��2=16���ɣ�a+b��2=��a��b��2+4ab��ab=3���������ʽa��b��ֵ��

 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�