题目内容
【题目】如图1,已知直线l1∥l2 , 且l1、l2分别相交于A、B两点,l4和l1、l2分别交于C、D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3.点P在线段AB上. 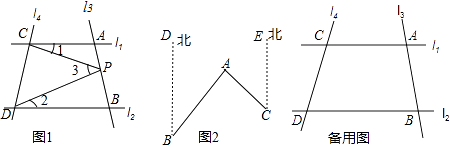
(1)若∠1=22°,∠2=33°,则∠3= .
(2)试找出∠1、∠2、∠3之间的等量关系,并说明理由.
(3)应用(2)中的结论解答下列问题: 如图2,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数.
(4)如果点P在直线l3上且在A、B两点外侧运动时,其他条件不变,试探究∠1、∠2、∠3之间的关系(点P和A、B两点不重合),直接写出结论即可.
【答案】
(1)55°
(2)解:∠1+∠2=∠3,
∵l1∥l2,
∴∠1+∠PCD+∠PDC+∠2=180°,
在△PCD中,∠3+∠PCD+∠PDC=180°,
∴∠1+∠2=∠3

(3)解:过A点作AF∥BD,则AF∥BD∥CE,则∠BAC=∠DBA+∠ACE=40°+45°=85°
(4)解:当P点在A的外侧时,如图2,
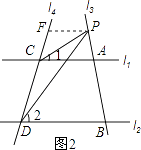
过P作PF∥l1,交l4于F,
∴∠1=∠FPC.
∵l1∥l4,
∴PF∥l2,
∴∠2=∠FPD
∵∠CPD=∠FPD﹣∠FPC
∴∠CPD=∠2﹣∠1.
当P点在B的外侧时,如图3,
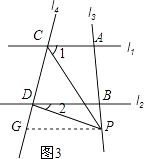
过P作PG∥l2,交l4于G,
∴∠2=∠GPD
∵l1∥l2,
∴PG∥l1,
∴∠1=∠CPG
∵∠CPD=∠CPG﹣∠GPD
∴∠CPD=∠1﹣∠2.
【解析】解:(1)∠1+∠2=∠3. ∵l1∥l2 ,
∴∠1+∠PCD+∠PDC+∠2=180°,
在△PCD中,∠3+∠PCD+∠PDC=180°,
∴∠3=∠1+∠2=55°,
所以答案是:55°;
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】某校航模小分队年龄情况如表所示,则这12名队员年龄的众数、中位数分别是( )
年龄(岁) | 12 | 13 | 14 | 15 | 16 |
人数 | 1 | 2 | 2 | 5 | 2 |
A. 2,14岁B. 2,15岁C. 19岁,20岁D. 15岁,15岁