题目内容
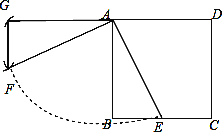
【题目】如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE绕点A顺时针旋转90°,设点E的对应点为F.

(1)画出旋转后的三角形.(尺规作图,保留作图痕迹,不写作法)
(2)求点E运动到点F所经过的路径的长
【答案】(1)作图见解析;(2)![]() .
.
【解析】
试题分析:(1)延长DA到G点,使AG=AB,然后分别以A、G为圆心,AE、BE为半径画弧,两弧相交于点F,则△AGF即为所作;
(2)点E运动到点F所经过的路径是以A点为圆心,AB为半径.圆心角为90°的弧,然后根据弧长公式求解.
试题解析:(1)如图,△AGF为所作;
(2)∵E是BC的中点,
∴BE=1,
∴AB=![]() ,
,
∵△ABE绕点A顺时针旋转90°得到△AGF,
∴∠EAF=90°,
∴点E运动到点F所经过的路径的长=![]() =
=![]() .
.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目