题目内容
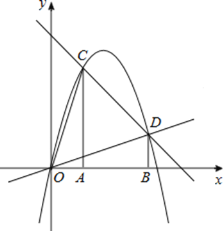
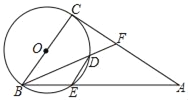
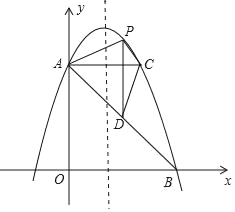
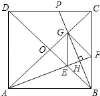
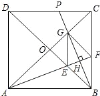
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)试判断四边形BEGF的形状并说明理由.
(2)求![]() 的值.
的值.
【答案】(1)四边形BEGF是菱形;(2)1+![]() .
.
【解析】
(1)先证明△AHG≌△AHB,得出GH=BH,由线段垂直平分线的性质得出EG=EB,FG=FB;再证出∠BEF=∠BFE,得出EB=FB,因此EG=EB=FB=FG,即可得出结论;
(2)设OA=OB=OC=a,菱形BEGF的边长为b,由菱形的性质CG=GF=b,(也可由△OAE≌△OBG得OG=OE=a﹣b,OC﹣CG=a﹣b,得CG=b);然后在Rt△GOE中,由勾股定理可得a和b的关系,通过相似三角形△CGP∽△AGB的对应边成比例得到:![]() ,即可得到答案.
,即可得到答案.
(1)四边形BEGF是菱形.理由如下:
∵∠GAH=∠BAH,AH=AH,∠AHG=∠AHB=90°,∴△AHG≌△AHB,∴GH=BH,∴AF是线段BG的垂直平分线,∴EG=EB,FG=FB.
∵∠BEF=∠BAF+∠ABE=67.5°,∠BFE=90°﹣∠BAF=67.5°,∴∠BEF=∠BFE,∴EB=FB,∴EG=EB=FB=FG,∴四边形BEGF是菱形.
(2)设OA=OB=OC=a,菱形BEGF的边长为b.
∵四边形BEGF是菱形,∴GF∥OB,∴∠CGF=∠COB=90°,∴∠GFC=∠GCF=45°,∴CG=GF=b.
∵四边形ABCD是正方形,∴OA=OB,∠AOE=∠BOG=90°
∵BH⊥AF,∴∠GAH+∠AGH=90°=∠OBG+∠AGH,∴∠GAH=∠OBG,∴△OAE≌△OBG,∴OG=OE=a﹣b,AE=BG.
∵在Rt△GOE中,GE![]() OG,∴b
OG,∴b![]() (a﹣b),整理得:a
(a﹣b),整理得:a![]() b,∴AC=2a=(2
b,∴AC=2a=(2![]() )b,AG=AC﹣CG=(1
)b,AG=AC﹣CG=(1![]() )b.
)b.
∵PC∥AB,∴△ABG∽△CPG,∴![]() ,∴
,∴![]() .
.

 阅读快车系列答案
阅读快车系列答案