题目内容
已知三点（3，5），（t，9），（-4，-9）在同一条直线上，则t=________．
5
分析：先求出过点（3，5），（-4，-9）的直线解析式，再把（t，9）代入解析式即可求出t的值．
解答：设过点（3，5），（-4，-9）的直线解析式为y=kx+b（k≠0），
则
，解得，
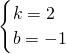，故过点（3，5），（-4，-9）的直线解析式为y=2x-1．
把（t，9）代入得：9=2t-1，
解得：t=5．
点评：本题考查用待定系数法确定函数解析式及一次函数图象上点的坐标特点．
分析：先求出过点（3，5），（-4，-9）的直线解析式，再把（t，9）代入解析式即可求出t的值．
解答：设过点（3，5），（-4，-9）的直线解析式为y=kx+b（k≠0），
则
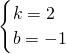，解得，，故过点（3，5），（-4，-9）的直线解析式为y=2x-1．把（t，9）代入得：9=2t-1，
解得：t=5．
点评：本题考查用待定系数法确定函数解析式及一次函数图象上点的坐标特点．
练习册系列答案
相关题目
已知三点A（2，3），B（5，4），C（-4，1），依次连接这三点，则（ ）
| A、构成等边三角形 | B、构成直角三角形 | C、构成锐角三角形 | D、三点在同一直线上 |
如图，在平面直角坐标系中，已知三点A（0，a），B（b，0），C（b，c），其中a，b，c满足关系式|a-2|+（b-3）2=0，c=2b-a；