题目内容
在平面直角坐标系中,已知三点A(0,a),B(b,0),C(b,c),其中a,b,c满足关系式|a-2|+(b-3)2=0,c=2b-a;
(1)求a,b,c的值.
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积;若四边形ABOP的面积与△ABC的面积相等,请求出点P的坐标;
附加题:
(3)若B,A两点分别在x轴,y轴的正半轴上运动,设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,那么,点A,B在运动的过程中,∠AQB的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.
(4)是否存在一点N(n,-1),使AN+NC距离最短?如果有,请求出该点坐标,如果没有,请说明理由.
(1)求a,b,c的值.
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积;若四边形ABOP的面积与△ABC的面积相等,请求出点P的坐标;
附加题:
(3)若B,A两点分别在x轴,y轴的正半轴上运动,设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,那么,点A,B在运动的过程中,∠AQB的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.
(4)是否存在一点N(n,-1),使AN+NC距离最短?如果有,请求出该点坐标,如果没有,请说明理由.
分析:(1)先根据非负数的性质求得a、b的值,再代入c=2b-a即可求出c的值;
(2)由于点P(m,1)在第二象限,所以四边形ABOP的面积=△AOP的面积+△AOB的面积;先根据三角形的面积公式求出△ABC的面积,再由四边形ABOP的面积与△ABC的面积相等列出关于m的方程,解方程求出m的值即可;
(3)根据角平分线的定义、三角形内角和定理及外角的性质求出∠AQB=45°,则∠AQB的大小不会发生变化;
(4)先作出点A关于直线y=-1的对称点A′(0,-4),连接A′C,交直线y=-1于点N,则AN+NC距离最短,再运用待定系数法求出直线A′C的解析式,将y=-1代入,求出的x的值即为N得到横坐标.
(2)由于点P(m,1)在第二象限,所以四边形ABOP的面积=△AOP的面积+△AOB的面积;先根据三角形的面积公式求出△ABC的面积,再由四边形ABOP的面积与△ABC的面积相等列出关于m的方程,解方程求出m的值即可;
(3)根据角平分线的定义、三角形内角和定理及外角的性质求出∠AQB=45°,则∠AQB的大小不会发生变化;
(4)先作出点A关于直线y=-1的对称点A′(0,-4),连接A′C,交直线y=-1于点N,则AN+NC距离最短,再运用待定系数法求出直线A′C的解析式,将y=-1代入,求出的x的值即为N得到横坐标.
解答:解:(1)∵|a-2|+(b-3)2=0,
∴a-2=0,b-3=0,
解得a=2,b=3.
将a=2,b=3代入c=2b-a,得
c=2×3-2=4.
故a=2,b=3,c=4;
 (2)如图.如果在第二象限内有一点P(m,1),
(2)如图.如果在第二象限内有一点P(m,1),
那么四边形ABOP的面积=△AOP的面积+△AOB的面积
=
×2×(-m)+
×3×2
=3-m;
∵△ABC的面积=
×4×3=6,
∴3-m=6,解得m=-3,
∴点P的坐标(-3,1);
 附加题:
附加题:
(3)如图.∠AQB的大小不会发生变化,理由如下:
∵∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,
∴∠1=
∠DAB,∠2=
∠ABE,
∴∠AQB=180°-(∠1+∠2)
=180°-
(∠DAB+∠ABE)
=180°-
(90°+∠ABO+90°+∠BAO)
=180°-
(90°+90°+90°)
=45°.
∴∠AQB的大小不会发生变化;
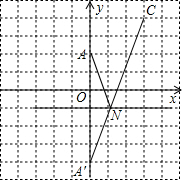 (4)存在一点N(
(4)存在一点N(
,-1),使AN+NC距离最短.理由如下:
如图,作出点A(0,2)关于直线y=-1的对称点A′(0,-4),连接A′C,交直线y=-1于点N,则AN+NC距离最短.
设直线A′C的解析式为y=kx+t,
将点A′(0,-4),C(3,4)代入,
得
,
解得
,
所以直线A′C的解析式为y=
x-4,
当y=-1时,
x-4=-1,
解得x=
,
即点N的坐标为(
,-1).
故存在一点N(
,-1),使AN+NC距离最短.
∴a-2=0,b-3=0,
解得a=2,b=3.
将a=2,b=3代入c=2b-a,得
c=2×3-2=4.
故a=2,b=3,c=4;
 (2)如图.如果在第二象限内有一点P(m,1),
(2)如图.如果在第二象限内有一点P(m,1),那么四边形ABOP的面积=△AOP的面积+△AOB的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=3-m;
∵△ABC的面积=
| 1 |
| 2 |
∴3-m=6,解得m=-3,
∴点P的坐标(-3,1);
 附加题:
附加题:(3)如图.∠AQB的大小不会发生变化,理由如下:
∵∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AQB=180°-(∠1+∠2)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=45°.
∴∠AQB的大小不会发生变化;
 (4)存在一点N(
(4)存在一点N(| 9 |
| 8 |
如图,作出点A(0,2)关于直线y=-1的对称点A′(0,-4),连接A′C,交直线y=-1于点N,则AN+NC距离最短.
设直线A′C的解析式为y=kx+t,
将点A′(0,-4),C(3,4)代入,
得
|
解得
|
所以直线A′C的解析式为y=
| 8 |
| 3 |
当y=-1时,
| 8 |
| 3 |
解得x=
| 9 |
| 8 |
即点N的坐标为(
| 9 |
| 8 |
故存在一点N(
| 9 |
| 8 |
点评:本题考查了非负数的性质,三角形的面积,三角形内角和定理,三角形外角的性质,轴对称-最短路线问题,运用待定系数法求函数的解析式,综合性较强,难度适中.根据非负数的性质求出a、b的值及运用轴对称的性质作出点N的位置是解题的关键.

练习册系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=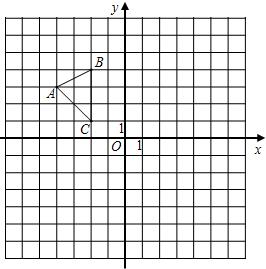 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.