Question

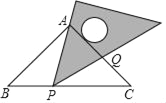
【题目】在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC＝2，直角三角板含45°角的顶点P在边BC上移动（点P不与B，C重合），如图，直角三角板的一条直角边始终经过点A，斜边与边AC交于点Q，当△ABP为等腰三角形时，CQ的长为_____．

Answer 1

【答案】1或2﹣2．

【解析】

由等腰直角三角形的性质得BCAB＝2，∠B＝∠C＝45°，再证明∠BAP＝∠CPQ，则可判断△CPQ∽△BAP，所以，分两种情况讨论：当PB＝PA时，易得AP⊥BC，BP＝CPBC，利用相似比可计算出CQ＝1；当BP＝AB＝2时，易得PC＝22，利用相似比可计算出此时CQ＝22．

∵△ABC为等腰直角三角形，∴BCAB＝2，∠B＝∠C＝45°．

∵∠APC＝∠B+∠BAP，即∠APQ+∠CPQ＝∠B+∠BAP，而∠APQ＝45°，∴∠BAP＝∠CPQ，∴△CPQ∽△BAP，∴．分两种情况讨论：

当PB＝PA时，则AP⊥BC，此时BP＝CPBC，∴CQ1；

当BP＝AB＝2时，此时PC＝22，∴CQ2．

综上所述：CQ的长为1或22．

故答案为：1或22．