Question

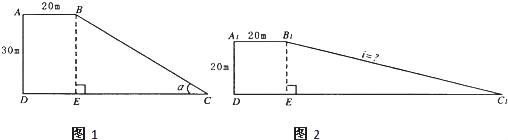
【题目】一段路基的横断面是直角梯形，如图1，已知原来坡面的坡角α的正弦值为0.6，现不改变土石方量，全部利用原有土石方进行坡面改造，使坡度变小，达到如右下图2的技术要求.试求出改造后坡面的坡度是多少？

Answer 1

【答案】(1) DC＝60 m；(2) 改造后坡面的坡角约为14.0°.

【解析】

由已知可求EC=40m．在不改变土石方量，全部充分利用原有土石方的前提下进行坡面改造，使坡度变小，则梯形ABCD面积=梯形A1B1C1D面积，可再求出EC1=80（m），即可求出改建后的坡度i=B1E：EC1=20：80=1：4．

(1)作BE⊥DC于E，得矩形ABED与Rt△BCE.

在Rt△BCE中，

∵sinα＝＝0.6，BE＝AD＝30 m，

∴BC＝＝50 m，

∴EC2＝BC2－BE2＝502－302＝1 600，

∴EC＝40 m，

∴DC＝DE＋EC＝20m＋40m＝60 m；

(2)作B1E1⊥D1C1于E1，在不改变土石方量，全部充分利用原有土石方的前提下进行坡面改造，使坡度变小，

则梯形ABCD面积＝梯形A1B1C1D面积，

即×(20＋60)×30＝×20(20＋20＋E1C1)，

解得E1C1＝80(m)，

所以改造后的坡度i＝B1E1∶E1C1＝20∶80＝1∶4，

∵tan 14.0°＝0.249 3，tan 14.1°＝0.251 1，

∴改造后坡面的坡角约为14.0°.