题目内容
【题目】如图,菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EG⊥CD于点G,则∠FGC= . 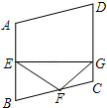
【答案】55°
【解析】解:延长GF,交AB的延长线于点P. ∵F为BC的中点,
∴BF=CF,
∵四边形ABCD为菱形,
∴AB∥DC,
∴∠PBF=∠GCF,∠BFP=∠CFG,
在△BPF与△CGF中,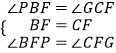 ,
,
∴△BPF≌△CGF,
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEG=90°,
∴EF= ![]() PG,
PG,
∵GF= ![]() PG,
PG,
∴EF=GF,
∴∠FEG=∠EGF,
∵∠BEG=∠EGC=90°,
∴∠BEG﹣∠FEG=∠EGC﹣∠EGF,即∠BEF=∠FGC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°﹣∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE= ![]() (180°﹣70°)=55°,
(180°﹣70°)=55°,
∴∠FGC=55°.
所以答案是55°.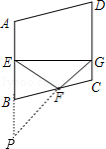
【考点精析】掌握菱形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目

