Question

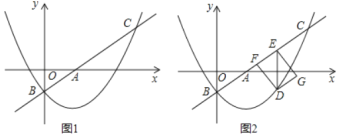
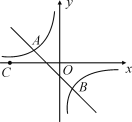
【题目】如图，点A（－2，n），B（1，－2）是一次函数y＝kx＋b的图象和反比例函数y＝的图象的两个交点．

（1）求反比例函数和一次函数的解析式；

（2）根据图象写出，当kx＋b<时，x的取值范围；

（3）若C是x轴上一动点，设t＝CB－CA，求t的最大值，并求出此时点C的坐标．

Answer 1

【答案】（1）反比例函数的解析式为，一次函数的解析式为；（2）或；（3）C点坐标为（－5，0），t的最大值为．

【解析】

（1）先将点代入反比例函数可求出其解析式，从而可得点A的坐标，再利用待定系数法可求出一次函数的解析式；

（2）根据点A、B的坐标，利用图象法求解即可得；

（3）如图（见解析），作点A关于x轴的对称点，从而可得点的坐标，再根据三角形的三边关系定理得出t取得最大值时，点的位置，然后利用两点之间的距离公式可求出t的最大值，又利用待定系数法求出直线的解析式，再令可求出点C的坐标．

（1）将点代入反比例函数得：，解得

则反比例函数的解析式为

当时，，即点

将，代入一次函数的解析式得：

解得

则一次函数的解析式为；

（2）表示的是一次函数的图象位于反比例函数图象的下方，求出此时的x取值范围即可

则结合，可得：或

故x的取值范围为或；

（3）如图，作点A关于x轴的对称点

则点的坐标为，

因此有

由三角形的三边关系定理得：

当且仅当三点共线时，t取得最大值，最大值为

由两点之间的距离公式得：

即t的最大值为

设直线的解析式为

将，代入得：

解得

则直线的解析式为

令得，解得

则点C的坐标为．