Question

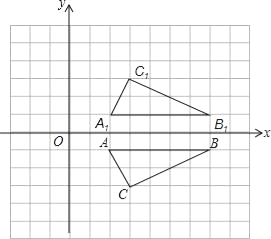
【题目】如图，已知坐标系中点A（2，-1），B（7，-1），C（3，-3）．

（1）判定△ABC的形状；

（2）设△ABC关于x轴的对称图形是△A1B1C1，若把△A1B1C1的各顶点的横坐标都加2．纵坐标不变，则△A1B1C1的位置发生什么变化？若最终位置是△A2B2C2，求C2点的坐标；

（3）试问在x轴上是否存在一点P，使PC-PB最大，若存在，求出PC-PB的最大值及P点坐标；若不存在，说明理由．

Answer 1

【答案】（1）△ABC是直角三角形；（2）图像向右平移2个单位，C2坐标为（5，2）；（3）y=x-；P(9，0).

【解析】

（1）计算出A，B，A，比较数量关系即可；

（2）把△的各顶点的横坐标都加2．纵坐标不变，则图形向右移动两个单位；

（3）连接C，与x轴的交点即为P，设BC对应一次函数为y=kx+b,联立方程组即可求出点P坐标．

本题解析:

解：（1）∵AC2=22+12=5，BC2=42+22=20，AB2=52

∴AC2+BC2=AB2

∴△ABC是直角三角形

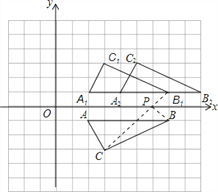
（2）图像向右平移2个单位，C2坐标为（5，2）

（3）存在.连接CB1，与x轴的交点即为P.

理由：设BC对应一次函数为y=kx+b

∵C（3，-3） B（7,-1）

∴

∴

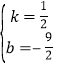
∴y=x-

令y=0得x=9

∴P(9，0)