题目内容
如图,△ABC是等腰直角三角形,AB= ,D为斜边BC上的一点(D与B、C均不重合
,D为斜边BC上的一点(D与B、C均不重合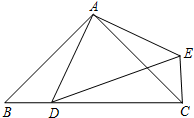 ),连接AD,把△ABD绕点A按逆时针旋转后得到△ACE,连接DE,设BD=x.
),连接AD,把△ABD绕点A按逆时针旋转后得到△ACE,连接DE,设BD=x.
(1)求证∠DCE=90°;
(2)当△DCE的面积为1.5时,求x的值;
(3)试问:△DCE的面积是否存在最大值?若存在,请求出这个最大值,并指出此时x的取值;若不存在,请说明理由.
解:(1)∵△ABD绕点A按逆时针旋转后得到△ACE,
∴△ACE≌△ABD,
∴∠ABD=∠ACE,
又∵△ABC是等腰直角三角形,且BC为斜边,
∴∠ABD+∠ACD=90°,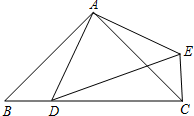
∴∠ACE+∠ACD=90°,
即:∠DCE=90°;
(2)∵AC=AB= ,
,
∴BC2=AC2+AB2=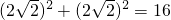 ,
,
∴BC=4.
∵△ACE≌△ABD,∠DCE=90°,
∴CE=BD=x,而BC=4,
∴DC=4-x,
∴Rt△DCE的面积为: DC•CE=
DC•CE= (4-x)x.
(4-x)x.
∴ (4-x)x=1.5,
(4-x)x=1.5,
即x2-4x+3=0.
解得x=1或x=3.
(3)△DCE存在最大值.
理由如下:设△DCE的面积为y,于是得y与x的函数关系式为:
y= (4-x)x(0<x<4),
(4-x)x(0<x<4),
=- (x-2)2+2,
(x-2)2+2,
∵a=- <0,
<0,
∴当x=2时,函数y有最大值2.
又∵x满足关系式0<x<4,
故当x=2时,△DCE的最大面积为2.
分析:(1)△ABC是等腰直角三角形,△ABD绕点A按逆时针旋转后得到△ACE,得到∠ABD与∠ACE相等,进而得到∠ACE+∠ACD=90°即证得;
(2)由直角三角形到△ACE≌△ABD,从而得直角三角形的面积公式而解得;
(3)通过函数式的判断来得到.
点评:本题主要考查了全等三角形的判定与性质,及一元二次方程、二次函数等基础知识,考查等价转换思想,运算求解等能力和创新意识等.
∴△ACE≌△ABD,
∴∠ABD=∠ACE,
又∵△ABC是等腰直角三角形,且BC为斜边,
∴∠ABD+∠ACD=90°,

∴∠ACE+∠ACD=90°,
即:∠DCE=90°;
(2)∵AC=AB=
 ,
,∴BC2=AC2+AB2=
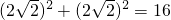 ,
,∴BC=4.
∵△ACE≌△ABD,∠DCE=90°,
∴CE=BD=x,而BC=4,
∴DC=4-x,
∴Rt△DCE的面积为:
 DC•CE=
DC•CE= (4-x)x.
(4-x)x.∴
 (4-x)x=1.5,
(4-x)x=1.5,即x2-4x+3=0.
解得x=1或x=3.
(3)△DCE存在最大值.
理由如下:设△DCE的面积为y,于是得y与x的函数关系式为:
y=
 (4-x)x(0<x<4),
(4-x)x(0<x<4),=-
 (x-2)2+2,
(x-2)2+2,∵a=-
 <0,
<0,∴当x=2时,函数y有最大值2.
又∵x满足关系式0<x<4,
故当x=2时,△DCE的最大面积为2.
分析:(1)△ABC是等腰直角三角形,△ABD绕点A按逆时针旋转后得到△ACE,得到∠ABD与∠ACE相等,进而得到∠ACE+∠ACD=90°即证得;
(2)由直角三角形到△ACE≌△ABD,从而得直角三角形的面积公式而解得;
(3)通过函数式的判断来得到.
点评:本题主要考查了全等三角形的判定与性质,及一元二次方程、二次函数等基础知识,考查等价转换思想,运算求解等能力和创新意识等.

练习册系列答案
相关题目
 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
 如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是
如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )
(2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )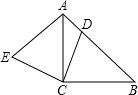 已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.
已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.