题目内容
【题目】在平面直角坐标系
中，若点
和点
关于
轴对称，点和
关于直线
对称，则称点是点关于轴，直线的“二次对称点”．
（1）已知点
，直线是经过
且平行于
轴的一条直线，则点
的“二次对称点”的坐标为______；
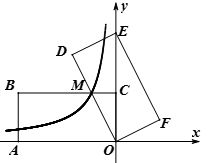
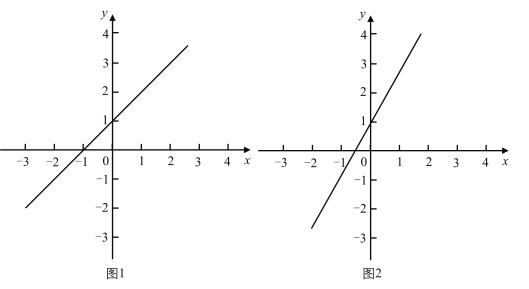
（2）如图1，直线经过
、
，点
的坐标为
．
①点关于轴，直线的“二次对称点”的坐标为______；
②当点在轴上移动，请你在图1中画出它关于轴，直线的“二次对称点”的运动路径．
（3）如图2，
是轴上的动点，线段
经过点
，且点
点
的坐标分别为
，直线经过且与轴负半轴夹角为60°，在点的运动过程中，若线段上存在点
，使得点
是点关于轴，直线的“二次对称点”，且点在轴上，则点的纵坐标
的取值范围是_____．
【答案】（1）（1，4）；（2）①（-1，-1）；②见解析；（3）-3＜
＜1
【解析】
（1）根据“二次对称点”的概念先算出A关于y轴对称点，再求出该点关于l的点即可；
（2）①求出直线l的解析式，从而根据定义得出结果；
②根据对称的性质可得运动路径是直线，从而求出该直线，画出即可；
（3）根据题意讨论当点N分别与点R和点S重合时，求出点N′的运动路径，再根据点N′在线段RS上得出的最大值和最小值即可.
解：（1）由题意可知：∵A（-1，0），
∴点A关于y轴对称的点A1坐标为（1，0），
∵l是经过（0，2）且平行于
轴的一条直线，即y=2，
∴点A关于
轴，直线
的“二次对称点”坐标为（1，4）；
（2）①∵直线经过
、
，
设直线l的解析式为y=kx+b，将、，代入
，
解得
，
∴直线l的解析式为：y=x+1，
∵点E（2，0），
由题意可得点E关于轴，直线的“二次对称点”为（-1，-1）；
②由关于轴，直线的“二次对称点”的定义可知，
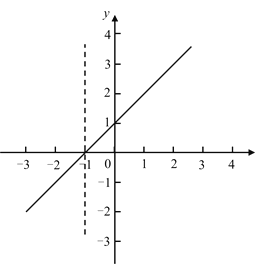
当点E在x轴运动时，点E关于y轴对称的点E1也在x轴上，
而点x轴关于直线l的对称图形为直线x=-1，
∴点E1关于直线l对称点在直线x=-1上，运动轨迹如图：
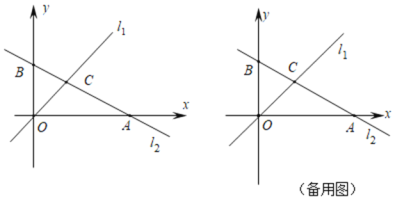
（3）∵直线经过且与轴正半轴夹角为60°，
如图，直线l与x轴交于点C，与y轴交于点B，
∴∠BCO=60°，
∴BC=2CO，
在△BCO中，BO2+CO2=BC2，BO=1，
解得：CO=
，即点C（
，0），
结合B（0，1），可求得：直线l的表达式：
，
当点N与点R重合， N（t，1），
由题意可知，如图，此时点N′的运动路径为l1，
∵∠CBO=90°-60°=30°，
∴∠N″BO=30°，
∵OB=1，
∴可知l1和l关于y轴对称，
∴l1的表达式为：y=
，
与y轴交点为（0，1）；
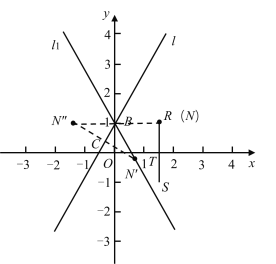
当点N和点S重合，N（t，-1），
由题意可知，如图，此时点N′的运动路径为l2，且l1∥l2，
设l2的解析式为y=
x+b1，
当N′在l1上时，将y=-1代入l1，
解得x=
，
此时N′坐标为（，-1），代入l2中，
解得b1=-3，
∴l2的解析式为y=x-3，
∴l2与y轴交点为（0，-3），
由题意可知当点N在线段RS上时，N′的运动轨迹皆为直线，且在l1和l2之间，
综上所述，的取值范围是：-3＜＜1.
