Question

如图，已知直线y=

1

4

x，与双曲线y=

k

x

（k＞0）交于A、B两点，且A点的横坐标为4．

（1）求k的值及B点的坐标；
（2）若双曲线y=

k

x

（k＞0）上一点C的纵坐标为2，求△AOC的面积；
（3）在x轴上找一点P，使以点O、C、P为顶点的三角形是等腰三角形，试写出P点的坐标．

Answer 1

（1）把x=4代入y=

1

4

x得y=1，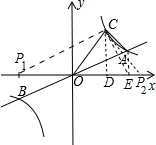
∴A点坐标为（4，1），
把A（4，1）代入y=

k

x

得k=4×1=4，
∵直线y=

1

4

x与双曲线y=

4

x

的交点关于原点对称，
∴B点坐标为（-4，-1）；

（2）作CD⊥x轴于D，AE⊥x轴于E，如图，
把x=2代入y=

4

x

得y=2，
∴C点坐标为（2，2），
∴S_△OCD=S_△OAE=

1

2

×4=2，
∵S_△OCD+S_梯形CDEA=S_△OAE+S_△AOC，
∴S_△AOC=

1

2

（1+2）（4-2）=3；

（3）∵C（2，2）
∴OC=2

2

，
当OC=OP时，△OCP是等腰三角形，即P点落在P₁或P₂的位置，此时P点坐标为（-2

2

，0）或（2

2

，0）；
当CO=CP时，△OCP是等腰三角形，即P点落在E点的位置，此时P点坐标为（4，0）；
当PO=PC时，△OCP是等腰三角形，即P点落在D点的位置，此时P点坐标为（2，0），
∴满足条件的P点坐标为（2

2

，0）、（-2

2

，0）、（4，O）、（2，0）．