题目内容
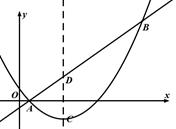
(10分)已知抛物线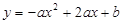 与
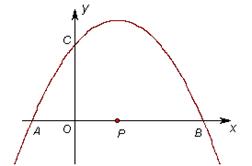
与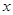 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
(1)直接写出抛物线的对称轴,及抛物线与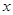 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
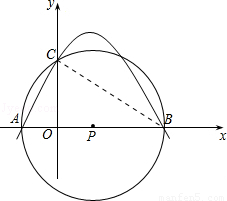
(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式;
(3)坐标平面内是否存在点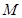 ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点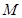 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 |
【答案】
见解析
【解析】
(1)根据对称轴公式,对称轴x=﹣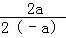 =1;
=1;
点B的坐标是(3,0).(2分)
(2)点C在以AB为直径的⊙P上,∴∠ACB=90°
由∠ACB=∠AOC=∠COB=90°得△AOC∽△COB,
∴ ,
,
∴CO= ,
,
∴b=
当x=﹣1,y=0时,﹣a﹣2a+ =0,
=0,
∴a=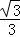 ,
,
∴y=﹣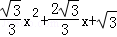 ;(6分)
;(6分)
(3)点M的坐标有三种情况,如果以AB为平行四边形的对角线,那么P(1,0)就是平行四边开的对称中心,即C点与M点关于P点位对称,设M点坐标为(x,y).
那么 ,x=2 .
,x=2 . 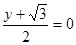 ,y=
,y= .∴M点坐标为(2,
.∴M点坐标为(2, )
)
同理以AC、BC为对称轴得出M点的坐标为(-4, )、(4,
)、(4, )
)
分别是:(2, ),(-4,
),(-4, )或(4,
)或(4, ).(10分)
).(10分)

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
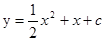 与x轴有两个不同的交点.
与x轴有两个不同的交点. .
.
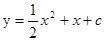 与x轴有两个不同的交点.
与x轴有两个不同的交点.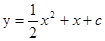 与x轴有两个不同的交点.
与x轴有两个不同的交点.