题目内容
(2011湖南衡阳,27,10分)已知抛物线 .
.
(1)试说明:无论m为何实数,该抛物线与x轴总有两个不同的交点;
(2)如图,当该抛物线的对称轴为直线x=3时,抛物线的顶点为点C,直线y=x-1与抛物线交于A、B两点,并与它的对称轴交于点D.
①抛物线上是否存在一点P使得四边形ACPD是正方形?若存在,求出点P的坐标;若不存在,说明理由;
②平移直线CD,交直线AB于点M,交抛物线于点N,通过怎样的平移能使得C、D、M、N为顶点的四边形是平行四边形.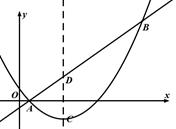
【解】(1) =
= =
= =
=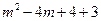 =
=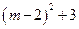 ,∵不管m为何实数,总有
,∵不管m为何实数,总有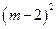 ≥0,∴
≥0,∴ =
=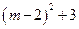 >0,∴无论m为何实数,该抛物线与x轴总有两个不同的交点.
>0,∴无论m为何实数,该抛物线与x轴总有两个不同的交点.
(2)∵抛物线的对称轴为直线x=3,∴ ,
,
抛物线的解析式为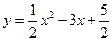 =
=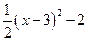 ,顶点C坐标为(3,-2),
,顶点C坐标为(3,-2),
解方程组 ,解得
,解得 或
或 ,所以A的坐标为(1,0)、B的坐标为(7,6),∵
,所以A的坐标为(1,0)、B的坐标为(7,6),∵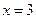 时y=x-1=3-1=2,∴D的坐标为(3,2),设抛物线的对称轴与
时y=x-1=3-1=2,∴D的坐标为(3,2),设抛物线的对称轴与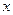 轴的交
轴的交 点为E,则E的坐标为(3,0),所以AE=BE=3,DE=CE=2,
点为E,则E的坐标为(3,0),所以AE=BE=3,DE=CE=2,
① 假设抛物线上存在一点P使得四边形ACPD是正方形,则AP、CD互相垂直 平分且相等,于是P与点B重合,但AP=6,CD=4,AP≠CD,故抛物线上不存在一点P使得四边形ACPD是正方形.
平分且相等,于是P与点B重合,但AP=6,CD=4,AP≠CD,故抛物线上不存在一点P使得四边形ACPD是正方形.
② (Ⅰ)设直线CD向右平移 个单位(
个单位( >0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3
>0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3 ,直线CD与直线y=x-1交于点M(3
,直线CD与直线y=x-1交于点M(3 ,2
,2 ),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
∵C、D、M、N为顶点的四边形是平行四边形,∴四边形CDMN是平行四边形或四边形CDNM是平行四边形.
(ⅰ)当四边形CDMN是平行四边形,∴M向下平移4个单位得N,
∴N坐标为(3 ,
, ),
),
又N在抛物线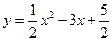 上,∴
上,∴ ,
,
解得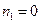 (不合题意,舍去),
(不合题意,舍去), ,
,
(ⅱ)当四边形CDNM是平行四边形,∴M向上平移4个单位得N,
∴N坐标为(3 ,
, ),
),
又N在抛物线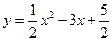 上,∴
上,∴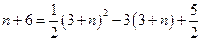 ,
,
解得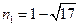 (不合题意,舍去),
(不合题意,舍去), ,
,
(Ⅱ) 设直线CD向左平移 个单位(
个单位( >0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3
>0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3 ,直线CD与直线y=x-1交于点M(3
,直线CD与直线y=x-1交于点M(3 ,2
,2 ),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
∵C、D、M、N为顶点的四边形是平行四边形,∴四边形CDMN是平行四边形或四边形CDNM是平行四边形.
(ⅰ)当四边形CDMN是平行四边形,∴M向下平移4个单位得N,
∴N坐标为(3 ,
,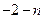 ),
),
又N在抛物线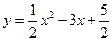 上,∴
上,∴ ,
,
解得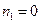 (不合题意,舍去),
(不合题意,舍去), (不合题意,舍去),
(不合题意,舍去),
(ⅱ)当四边形CDNM是平行四边形,∴M向上平移4个单位得N,
∴N坐标为(3 ,
,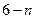 ),
),
又N在抛物线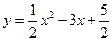 上,∴
上,∴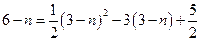 ,
,
解得 ,
, (不合题意,舍去),
(不合题意,舍去),
综上所述,直线CD向右平移2或(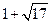 )个单位或向左平移(
)个单位或向左平移(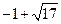 )个单位,可使得C、D、M、N为顶点的四边形是平行四边形.
)个单位,可使得C、D、M、N为顶点的四边形是平行四边形.
解析

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.

 的直径
的直径 过弦
过弦 的中点G,∠EOD=40°,则∠FCD的度数为 .
的中点G,∠EOD=40°,则∠FCD的度数为 .