Question

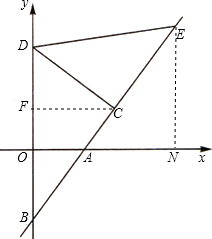
如图所示，直线AB交x轴于点A，交y轴于点B，点C、E在直线AB上，过点C作直线AB的垂线交y轴于点D，且OD=CD=CE．点C的坐标为（a，b），a、b（a＞b）是方程x²-12x+32=0的解．
（1）求DC的长；
（2）求直线AB的解析式；
（3）在x轴的正半轴上是否存在点Q，使△OCB和△OCQ相似？若存在，请直接写出Q点坐标；若不存在，请说明理由．

Answer 1

（1）解方程x²-12x+32=0得：
x₁=8，x₂=4，
∴C点坐标是（8，4），
过C作CF⊥y轴于F，
在Rt△DFC中，设DO=CO=y，则DF=y-4，CF=8，由勾股定理得：
（y-4）²+8²=y²，
解得：y=10，
即DC=10；

（2）过点E作EN⊥OA交射线FC于点N，交射线AO与H，则NH=4，
易证△DFC≌△CNE，得CN=DF=6，EN=FC=8，
∴E点坐标是（14，12），
设直线AB的解析式为y=kx+b，
把C（8，4），E（14，12）代入得：

12=14k+b 4=8k+b

，
解得：

k= 4 3 b=- 20 3

，
∴y_AB=

4

3

x-

20

3

；

（3）存在，
Q₁（

40

3

，0），Q₂（6，0）．