题目内容
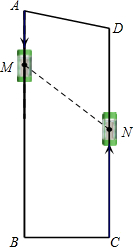 (2011•安宁市一模)随着科学技术的不断发展,人们的出行购物将会变得便捷、轻松,下图是我市未来购物商场的两部电梯的抽象图.已知:AB⊥BC于B,DC⊥BC于C,AB=26米,DC=24米,BC=8米.电梯M从A出发以1米/秒的速度匀速向下移动,同时,电梯N从C出发以2米/秒的速度匀速向上移动.因电梯还处在测试阶段,测试人员为了很好地测试电梯,规定当一个电梯到达另一个端点时,两部电梯停止移动.设电梯移动时间为t秒,请你帮测试人员先算一算:
(2011•安宁市一模)随着科学技术的不断发展,人们的出行购物将会变得便捷、轻松,下图是我市未来购物商场的两部电梯的抽象图.已知:AB⊥BC于B,DC⊥BC于C,AB=26米,DC=24米,BC=8米.电梯M从A出发以1米/秒的速度匀速向下移动,同时,电梯N从C出发以2米/秒的速度匀速向上移动.因电梯还处在测试阶段,测试人员为了很好地测试电梯,规定当一个电梯到达另一个端点时,两部电梯停止移动.设电梯移动时间为t秒,请你帮测试人员先算一算:(1)当t=
8
8
秒时,MN∥AD(只作回答不用书写过程);(2)当t=
| 26 |
| 3 |
| 26 |
| 3 |
(3)当t=
| 28 |
| 3 |
| 28 |
| 3 |
分析:AM=t,BM=26-t,CN=2t,DN=24-2t(0≤t≤12)
(1)因为AB∥DC,当AM=DN时,四边形AMND为平行四边形,得到MN∥AD,即t=24-2t,解方程即可;
(2)因为AB∥DC,当BM=CN时,四边形AMND为矩形,得到MN=BC,即26-t=2t,解方程即可;
(3)过D、N分别作AB的垂线,垂足分别为E、F,由∠AMN=∠MAD,得梯形ADNM为等腰梯形,则AE=MF,在Rt△AED中,AE=AB-BE=AB-DC=26-24=2,而BM=26-t,CN=2t,
得FM=2t-(26-t)=3t-26,则得到关于t的方程3t-26=2,解方程即可.
(1)因为AB∥DC,当AM=DN时,四边形AMND为平行四边形,得到MN∥AD,即t=24-2t,解方程即可;
(2)因为AB∥DC,当BM=CN时,四边形AMND为矩形,得到MN=BC,即26-t=2t,解方程即可;
(3)过D、N分别作AB的垂线,垂足分别为E、F,由∠AMN=∠MAD,得梯形ADNM为等腰梯形,则AE=MF,在Rt△AED中,AE=AB-BE=AB-DC=26-24=2,而BM=26-t,CN=2t,
得FM=2t-(26-t)=3t-26,则得到关于t的方程3t-26=2,解方程即可.
解答:解:(1)8;
(2)
;
(3)如图,过D、N分别作AB的垂线,垂足分别为E、F,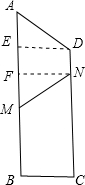
∵∠AMN=∠MAD,
∴梯形ADNM为等腰梯形,
∴AE=MF,
在Rt△AED中,AE=AB-BE=AB-DC=26-24=2,
而BM=26-t,CN=2t,
∴FM=2t-(26-t)=3t-26,
∴3t-26=2,
∴t=
.
故答案为:8;
;
.
(2)
| 26 |
| 3 |
(3)如图,过D、N分别作AB的垂线,垂足分别为E、F,

∵∠AMN=∠MAD,
∴梯形ADNM为等腰梯形,
∴AE=MF,
在Rt△AED中,AE=AB-BE=AB-DC=26-24=2,
而BM=26-t,CN=2t,
∴FM=2t-(26-t)=3t-26,
∴3t-26=2,
∴t=
| 28 |
| 3 |
故答案为:8;
| 26 |
| 3 |
| 28 |
| 3 |
点评:本题考查了直角梯形的性质:有一组对边平行,另一组对边不平行,且有一个直角.也考查了矩形的性质、平行四边形的判定与性质以及等腰梯形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011•安宁市一模)如图,直径AB=6的半圆,以点A为旋转中心将半圆逆时针旋转30°,使点B旋转到点C,则图中阴影部分的面积是( )
(2011•安宁市一模)如图,直径AB=6的半圆,以点A为旋转中心将半圆逆时针旋转30°,使点B旋转到点C,则图中阴影部分的面积是( )