题目内容
【题目】如图,抛物线的顶点为C(﹣1,﹣1),且经过点A、点B和坐标原点O,点B的横坐标为﹣3.
(1)求抛物线的解析式.
(2)求点B的坐标及△BOC的面积.
(3)若点D为抛物线上的一点,点E为对称轴上的一点,且以点A、O、D、E为顶点的四边形为平行四边形,请在左边的图上标出D和E的位置,再直接写出点D的坐标.

【答案】(1)y=(x+1)2﹣1 (2)(﹣3,3),3 (3)答案见解析
【解析】
(1)根据顶点坐标设出抛物线的顶点解析式,将原点坐标代入求出a的值,即可确定出抛物线的解析式.
(2)根据点B的横坐标,代入抛物线解析式求得点B坐标;过点B作BM⊥y轴于点M,过点C作CN⊥y轴于点N,构建一个直角梯形,进而求出△BOC的面积.
(3)根据题意分三种情况考虑,D在第一象限,第二象限以及第三象限,利用平行四边形的性质和坐标与图形的性质求出D的坐标即可.
解:(1)设抛物线解析式为y=a(x+1)2﹣1,
将点O(0,0)代入,得:a﹣1=0,
解得:a=1,
则抛物线解析式为y=(x+1)2﹣1;
(2)当x=﹣3时,y=3,
所以点B坐标为(﹣3,3),
如图1,过点B作BM⊥y轴于点M,过点C作CN⊥y轴于点N,
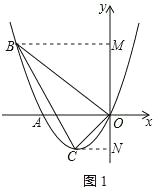
则BM=OM=3,CN=ON=1,
∴MN=4,
则S△BOC=S梯形BMNC﹣S△BOM﹣S△CON
=![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×3×3﹣
×3×3﹣![]() ×1×1
×1×1
=3;
(3)如图2所示,
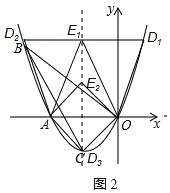
分三种情况考虑:
当D1在第一象限时,若四边形AOD1E1为平行四边形,
∴AO=E1D1=2,
∵抛物线对称轴为直线x=﹣1,
∴D1横坐标为1,
将x=1代入抛物线y=x2+2x=1+2=3,即D1(1,3);
当D2在第二象限时,同理D2(﹣3,3);
当D3在第三象限时,若四边形AE2OD3为平行四边形,此时D3与C重合,即D3(﹣1,﹣1);
综上,点D的坐标为(1,3)或(﹣3,3)或(﹣1,﹣1).

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;
(2)当﹣![]() <x<2时,y<0;
<x<2时,y<0;
(3)a﹣b+c=0;
(4)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧
则其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4