题目内容
 将边长分别为2、4、6的三个正三角形按如图方式排列,A、B、C、D在同一直线上,则图中阴影部分的面积的和为________.
将边长分别为2、4、6的三个正三角形按如图方式排列,A、B、C、D在同一直线上,则图中阴影部分的面积的和为________.

分析:根据等边三角形的每一个角都是60°,同位角相等两直线平行可得BE∥CF∥DG,再根据平行线分线段成比例定理求出BE=1,CF=3,然后可得两个阴影部分的面积等于△BEH与第二个等边三角形中的阴影部分的面积的和,再求出第二个等边三角形的高,然后两腰三角形的面积公式进行求解即可.
解答:
 解:如图,在三个正三角形中,∠ABE=∠BCF=∠CDG=60°,
解:如图,在三个正三角形中,∠ABE=∠BCF=∠CDG=60°,∴BE∥CF∥DG,
∴
 =
= ,
,即
 =
= ,
,解得CF=3,
∴第二个三角形中的阴影部分三角形的底边长为4-3=1,
同理
 =
= ,
,即
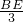 =
= ,
,解得BE=1,
边长为4的等边三角形的高为:4×
 =2
=2 ,
,∴阴影部分的面积的和=△BEH的面积+第二个等边三角形中的阴影部分的面积,
即
 ×1×2
×1×2 =
= .
.故答案为:
 .
.点评:本题主要考查了等边三角形的性质,三角形的面积,求出两阴影部分的三角形的边长得到阴影部分的面积等于“△BEH的面积+第二个等边三角形中的阴影部分的面积”是解题的关键.

练习册系列答案
相关题目
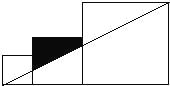 将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为
将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为
 已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2-b2的值.
已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2-b2的值.