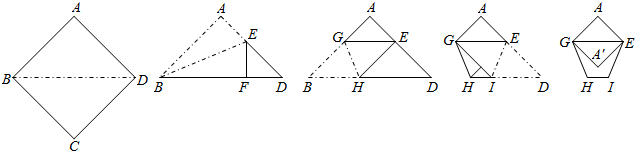
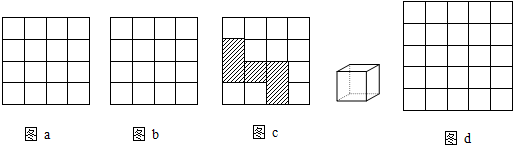
题目内容

将边长分别为
2
、2
2
、3
2
、4
2
、…的正方形的面积分别记作S1、S2、S3、S4，…，计算S2-S1，S3-S2，S4-S3，…．若边长为n•
2
（n为正整数）的正方形面积记作Sn，根据你的计算结果，猜想Sn-Sn-1=
4n-2
4n-2
．（用含n的式子表示）
分析：正方形的面积是边长的平方，我们先暂不考虑
2
，它们相邻面积的差就是
2
的“系数”的平方差，由此规律解决问题．
解答：解：S2-S1=（2
2
）2-（
2
）2=2×（22-12）=6；
S3-S2=（3
2
）2-（2
2
）2=2×（32-22）=10；
S4-S3=（4
2
）2-（3
2
）2=2×（42-32）=14；
…
Sn-Sn-1=（n
2
）2-[（n-1）
2
]2=2×[n2-（n-1）2]=4n-2．
故答案为：4n-2．
点评：此题主要考查了利用数据以及正方形的面积计算发现数据之间的规律，利用规律解决问题．
练习册系列答案
相关题目
将边长分别为
2
，2
2
，3
2
，4
2
…的正方形的面积记作S1，S2，S3，S4…，计算S2-S1，S3-S2，S4-S3…．若边长为n
2
（n为正整数）的正方形面积记作Sn，根据你的计算结果，猜想Sn+1-Sn=
 
．
如果正方形网格中的每一个小正方形边长都是1，则每个小格的顶点叫做格点．
（1）在图a中以格点为顶点画一个三角形，使三角形的三边长分别为3、
5
、2
2
；
（2）在图b中以格点为顶点画一个面积为10的正方形；
（3）观察图c中带阴影的图形，请你将它适当剪开，重新拼成一个正方形；（要求：在图c中用虚线作出，并用文字说明剪拼方法）图c说明：
沿虚线剪开，然后①、②、③分别对应拼接
沿虚线剪开，然后①、②、③分别对应拼接
．
（4）观察正方体，沿着一些棱将它剪开，展开成平面图形．若正方体的表面积为12，请你在图d中以格点为顶点画出一个正方体的平面展开图．（只需画出一种情形）
按照图示的方式可以将一张正方形纸片拆成一个环保纸袋（如图所示）．AB=
2
，则折成后纸袋的边AE和HI的长分别为
2-
2
2-
2
、
6-4
2
6-4
2
．
如果正方形网格中的每一个小正方形边长都是1，则每个小格的顶点叫做格点．
（1）在图a中以格点为顶点画一个三角形，使三角形的三边长分别为3、
5
、2
2
；
（2）在图b中以格点为顶点画一个面积为10的正方形；
（3）观察图c中带阴影的图形，请你将它适当剪开，重新拼成一个正方形；（要求：在图c中用虚线作出，并用文字说明剪拼方法）图c说明：______．
（4）观察正方体，沿着一些棱将它剪开，展开成平面图形．若正方体的表面积为12，请你在图d中以格点为顶点画出一个正方体的平面展开图．（只需画出一种情形）

精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网