题目内容
【题目】如图直线l：y＝kx+6与x轴、y轴分别交于点B、C两点，点B的坐标是（﹣8，0），点A的坐标为（﹣6，0）．
（1）求k的值．
（2）若点P是直线l在第二象限内一个动点，当点P运动到什么位置时，△PAC的面积为3，求出此时直线AP的解析式．
（3）在x轴上是否存在一点M，使得△BCM为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
【答案】（1）
，（2）P（﹣4，3）；y＝
x+9．（3）（﹣18，0），（﹣
，0），（2，0）或（8，0），见解析.
【解析】
（1）由点B的坐标，利用一次函数图象上点的坐标特征可求出k值；
（2）利用一次函数图象上点的坐标特征求出点C的坐标，设点P的坐标为（x，x+6），由S△PAC＝S△BOC﹣S△BAP﹣S△AOC结合△PAC的面积为3，可得出关于x的一元一次方程，解之即可得出点P的坐标，再利用待定系数法即可求出此时直线AP的解析式；
（3）利用勾股定理求出BC的长度，分CB＝CM，BC＝BM，MB＝MC三种情况考虑：①当CB＝CM时，由OM1＝OB＝8可得出点M1的坐标；②当BC＝BM时，由BM2＝BM3＝BC＝10结合点B的坐标可得出点M2，M3的坐标；③当MB＝MC时，设OM＝t，则M4B＝M4C＝8﹣t，利用勾股定理可得出关于t的一元一次方程，解之即可得出点M4的坐标．综上，此题得解．
（1）∵直线l：y＝kx+6过点B（﹣8，0），
∴0＝﹣8k+6，
∴k＝．
（2）当x＝0时，y＝x+6＝6，
∴点C的坐标为（0，6）．
依照题意画出图形，如图1所示，
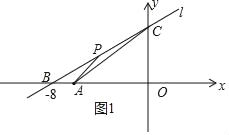
设点P的坐标为（x，x+6），
∴S△PAC＝S△BOC﹣S△BAP﹣S△AOC，
＝
×8×6﹣×2（x+6）﹣×6×6，
＝﹣x＝3，
∴x＝﹣4，
∴点P的坐标为（﹣4，3）．
设此时直线AP的解析式为y＝ax+b（a≠0），
将A（﹣6，0），P（﹣4，3）代入y＝ax+b，
得：
，解得：
，
∴当点P的坐标为（﹣4，3）时，△PAC的面积为3，此时直线AP的解析式为y＝x+9．
（3）在Rt△BOC中，OB＝8，OC＝6，
∴BC＝
＝10．
分三种情况考虑（如图2所示）：
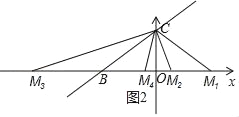
①当CB＝CM时，OM1＝OB＝8，
∴点M1的坐标为（8，0）；
②当BC＝BM时，BM2＝BM3＝BC＝10，
∵点B的坐标为（﹣8，0），
∴点M2的坐标为（2，0），点M3的坐标为（﹣18，0）；
③当MB＝MC时，设OM＝t，则M4B＝M4C＝8﹣t，
∴CM42＝OM42+OC2，即（8﹣t）2＝t2+62，
解得：t＝，
∴点M4的坐标为（﹣，0）．
综上所述：在x轴上存在一点M，使得△BCM为等腰三角形，点M的坐标为（﹣18，0），（﹣，0），（2，0）或（8，0）．
