题目内容
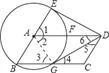
【题目】如图,平行四边形ABCD中,以A为圆心,AB为半径的圆交AD于F,交BC于G,延长BA交圆于E.
(1)若ED与⊙A相切,试判断GD与⊙A的位置关系,并证明你的结论;
(2)在(1)的条件不变的情况下,若GC=CD,求∠C.

【答案】GD与⊙A相切.理由见解析;(2) 120°
【解析】分析:(1)连接![]() ,由角的等量关系可以证出∠1=∠2,然后证明
,由角的等量关系可以证出∠1=∠2,然后证明![]() ≌
≌![]() 得到
得到![]()
(2)由(1)知![]() 根据角间的等量关系,解出∠6,继而求出
根据角间的等量关系,解出∠6,继而求出![]() 的值.
的值.
详解:(1)结论:GD与⊙O相切。理由如下:
连接AG.
∵点G、E在圆上,
∴AG=AE.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠B=∠1,∠2=∠3.
∵AB=AG,
∴∠B=∠3.
∴∠1=∠2.
在△AED和△AGD中,

∴△AED≌△AGD.
∴∠AED=∠AGD.
∵ED与⊙A相切,
∴![]()
∴![]()
∴AG⊥DG.
∴GD与⊙A相切.
(2)∵GC=CD,四边形ABCD是平行四边形,
∴AB=DC,∠4=∠5,AB=AG.
∵AD∥BC,
∴∠4=∠6.
∴![]()
∴∠2=2∠6.
∴![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目