题目内容
已知：二次函数y=ax2+bx+c（a≠0）中的x，y满足下表：
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | m | … |
（2）若A（p，y1），B（p+1，y2）两点都在该函数的图象上，且p＜0，试比较y1与y2的大小．
解：（1）由已知表格可得
函数的对称轴为x=1，
∴m=0；
（2）∵p＜0，
∴p＜p+1＜1，
∵对称轴为x=1，
A、B两点位于对称轴的左侧，
又因为抛物开口向上，
∴y1＞y2．
故答案为0，y1＞y2．
分析：观察表格知x=1是二次函数的对称轴，x=3关于x=-1对称，可得m=0，根据函数的增减性来判断较y1与y2的大小．
点评：此题主要考查一元二次方程与函数的关系，函数与x轴的交点的横坐标就是方程的根，此题从表格中找函数的对称轴，从而来运用函数的增减性来解题．
函数的对称轴为x=1，
∴m=0；
（2）∵p＜0，
∴p＜p+1＜1，
∵对称轴为x=1，
A、B两点位于对称轴的左侧，
又因为抛物开口向上，
∴y1＞y2．
故答案为0，y1＞y2．
分析：观察表格知x=1是二次函数的对称轴，x=3关于x=-1对称，可得m=0，根据函数的增减性来判断较y1与y2的大小．
点评：此题主要考查一元二次方程与函数的关系，函数与x轴的交点的横坐标就是方程的根，此题从表格中找函数的对称轴，从而来运用函数的增减性来解题．
练习册系列答案
阅读快车系列答案
相关题目
已知：二次函数的表达式为y=2x2+4x-1．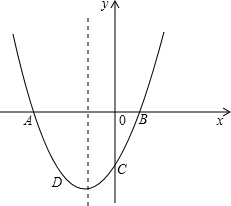
交于点C，点D（-2，-3）在抛物线上．