题目内容
【题目】如图，在平面直角坐标系xoy中，点A(3，3)，点B(4，0)，点C(0，-1)．
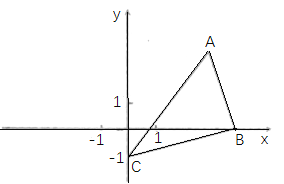
（1）以点C为中心，把△ABC逆时针旋转90°，画出旋转后的图形△A’B’C’(要求尺规作图，不写作法，保留作图痕迹)；
（2）在（1）的条件下，
①点A经过的路径AA’的长为________；(结果保留
)
②写出B’的坐标为________．
【答案】（1）见解析；（2）①
；②（-1，3）
【解析】
（1）根据旋转的定义分别作出点A、B饶点C逆时针旋转90°所得的对应点，再顺次连结即可.
（2）①根据（1）中所作的图求得半径AC的长，再由扇形的弧长公式即可得出答案；②由（1）中所作图即可得出答案.
解：（1）如图所示：△A＇B＇C＇即为所求.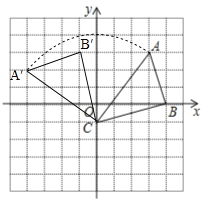
（2）①依题可得：
AC=
=5，∠ACA＇=90°，
∴点A经过的路径AA＇长为：
=
.
故答案为：.
②由图可知B＇坐标为（-1，3）.
故答案为：（-1，3）.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】运动员将小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度h（m）与它的飞行时间t（s）满足二次函数关系，t与h的几组对应值如下表所示．
t（s） | 0 | 0.5 | 1 | 1.5 | 2 | … |
h（m） | 0 | 8.75 | 15 | 18.75 | 20 | … |
（1）求h与t之间的函数关系式（不要求写t的取值范围）；
（2）求小球飞行3s时的高度；
（3）问：小球的飞行高度能否达到22m？请说明理由．
