题目内容
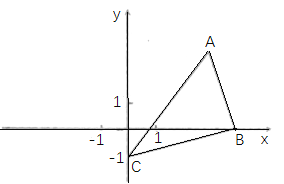
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=CD,∠ACD=α,将线段CD绕点C顺时针旋转90°得到线段CE,连接DE,AE,BD.
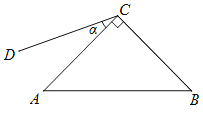
(1)依题意补全图形;
(2)判断AE与BD的数量关系与位置关系并加以证明;
(3)若60°<α≤110°,AB=4,AE与BD相交于点G,直接写出点G到直线AB的距离d的取值范围.
【答案】(1)详见解析;(2)AE=BD,AE⊥BD,证明详见解析;(3)![]() <d≤2.
<d≤2.
【解析】
(1)由旋转的性质即可得出结论;
(2)由旋转的性质得出∠ACE=∠BCD,AC=BC=CE=CD,进而判断出AE=BD,∠CAE=∠CBD,最后用三角形的内角和定理即可得出结论;
(3)先判断出点G是以AB为直径的圆上的一段弧,再用等腰三角形的性质求出∠ACE,进而得出∠BAG,即可得出结论.
解:(1)补全图形如图1所示,
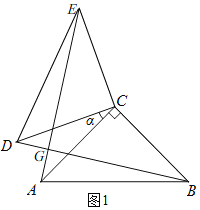
(2)如图1,由旋转知,CE=CD,∠DCE=90°=∠ACB,
∴∠ACE=∠BCD,
∵AC=BC=CD,
∴AC=BC=CE=CD,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠CBD,
在△ABC中,∠ACB=90°,AC=BC,
∴∠ABC=∠BAC=45°,
∴∠BAG+∠ABG=∠BAC+∠CAE+∠ABG=∠BAC+∠CBD+∠ABG=∠BAC+∠ABC=90°,
∴∠AGB=90°,
∴AE⊥BD,
即:AE=BD,AE⊥BD;
(3)由(2)知,∠AGB=90°,
∴点G在以AB为直径的圆上,如图2,
∵60°<α≤110°,
∴点G在弧GCG'上(不包括点G,包括点G'),
∵AC=BC,
∴点C到直径AB的距离为2,
即:点G到AB的最大距离为2,
当α=60°时,即:∠ACD=60°,
由旋转知,∠DCE=90°,
∴∠ACD+∠DCE=60°+90°=150°<180°,
∴点G在AC左侧,
∴∠ACE=60°+90°=150°,
由(2)知,AC=CE,
∴∠CAE=![]() (180°﹣∠ACE)=15°,
(180°﹣∠ACE)=15°,
∴∠BAG=BAC+∠CAE=60°,
∴∠ABG=90°﹣∠BAG=30°,
∵AB=4,
∴AG=2,
过点G作GH⊥AB于H,
∴∠AHG=90°,
∴GH=AGcos∠BAG=2×![]() =
=![]() ,
,
当α=110°时,即:∠ACD'=110°,
由旋转知,∠D'CE'=90°,
∴∠ACD'+∠D'CE'=200°,此时,点G'在BC右侧,
∴∠ACE'=360°﹣200°=160°,
∴∠CAE'=![]() (180°﹣∠ACE')=10°,
(180°﹣∠ACE')=10°,
∴∠BAG'=45°﹣10°=35°>30°,
过点G'作G'H'于H',
∴G'H'>GH,
p>∴点G到直线AB的距离d的取值范围为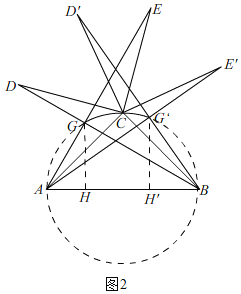

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案