题目内容
已知AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为R.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=R2.(提示:作直径FQ交⊙O于Q,并连结DQ)
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
(1)连接FO并延长交⊙O于Q,连接DQ 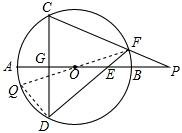
∵FQ是⊙O直径
∴∠FDQ=90°
∴∠QFD+∠Q=90°
∵CD⊥AB
∴∠P+∠C=90°
∵∠Q=∠C
∴∠QFD=∠P
∵∠FOE=∠POF
∴△FOE∽△POF
∴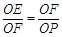
∴OE·OP=OF2=R2;
(2)成立
解析试题分析:(1)连接FO并延长交⊙O于Q,连接DQ.先根据同角的余角相等得到∠QFD=∠P,再结合公共角即可证明△FOE∽△POF,然后根据相似三角形的性质即可得到结果;
(2)依题意画出图形,连接FO并延长交⊙O于M,连接CM.根据圆周角定理及等角的余角相等可得∠CFM=∠E,再结合公共角即可证明△FOE∽△POF,然后根据相似三角形的性质即可得到结果.
(1)连接FO并延长交⊙O于Q,连接DQ. 
∵FQ是⊙O直径
∴∠FDQ=90°
∴∠QFD+∠Q=90°
∵CD⊥AB
∴∠P+∠C=90°
∵∠Q=∠C
∴∠QFD=∠P
∵∠FOE=∠POF
∴△FOE∽△POF
∴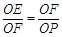
∴OE·OP=OF2=R2;
(2)如图,依题意画出图形,连接FO并延长交⊙O于M,连接CM
∵FM是⊙O直径
∴∠FCM=90°
∴∠M+∠CFM=90°
∵CD⊥AB
∴∠E+∠D=90°
∵∠M=∠D
∴∠CFM=∠E
∵∠POF=∠FOE
∴△POF∽△FOE
∴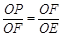
∴OE·OP=OF2=R2.
考点:本题考查的是相似三角形的性质与判定、垂径定理,圆周角定理
点评:解答本题的关键是熟练掌握直径所对的圆周角是直角;同角或等角的余角相等;同时熟记相似三角形的性质:相似三角形的对应边成比例,同时注意对应字母写在对应位置上.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD= 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.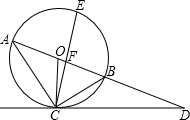

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,