题目内容
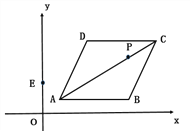
【题目】已知菱形ABCD在平面直角坐标系的位置如图所示，A（1，1），B(6,1),AC=4
，点P是对角线AC上的一个动点，E（0，2），当
周长最小时，点P的坐标为（ ）.
A. （2，2） B. （2， 
） C. （
， 
） D. （
， 
）
【答案】D
【解析】试题分析：连接ED，根据菱形的对称性，可得D与B对称，可得DP=BP，所以EB为EP+DP最短，几次是△EPD的周长最小，连接BD交AC于O，过O作OF⊥AB于F，可知AO=2
，AC⊥BD，根据勾股定理可求得BO=
=
，因此可求得OF=2，AF=4，然后由A、B点的可知AB∥x轴，即直线BA与x轴间的距离为1，所以可求得O点的坐标为（5,3），求得AC的解析式为
，然后由E（0,2）B（6,1）可得BE的解析式为
，联立方程组可求得x=
，y=
，因此P点坐标为（
， 
）.
故选：D.
练习册系列答案
相关题目
