题目内容
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BO E=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有(填序号)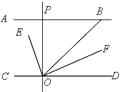
【答案】①②③
【解析】∵AB∥CD,
∴∠ABO=∠BOD=40°,
∴∠BOC=180°﹣40°=140°,
∵OE平分∠BOC,
∴∠BOE=70°;所以①正确;
∵OF⊥OE,
∴∠E OF=90°,
∴∠ BOF=90°﹣70°=20°,
∴∠BOF=∠BOD,所以②正确;
∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=20°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=70°﹣∠POE=50°,
而∠DOF=20 °,所以④错误.
故答案为①②③.
根据二直线平行内错角相等得出∠ABO=∠BOD=40°,根据邻补角的定义得出∠BOC=180°﹣40°=140°,根据角平分线的性质得出∠BOE=70° ,根据垂直的定义及角的和差得出∠ BOF=90°﹣70°=20° ,进而得出∠BOF=∠BOD ,根据垂直的定义及角的和差得出∠POE=90°﹣∠EOC=20°,从而得出∠POE=∠BOF;进而得出∠POB=70°﹣∠POE=50°,而∠DOF=20 ° 故∠POB≠2∠DOF 。

练习册系列答案
相关题目