题目内容
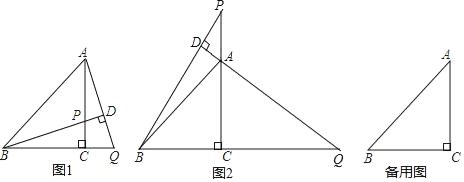
【题目】魔术大师夏尔
巴比耶90岁时定义了一个魔法三角阵，三角阵中含有四个区域（三个“边区域”和一个“核心区域”，如图1中的阴影部分），每个区域都含有5个数，把差相同的连续九个正整数填进三角阵中，每个区域的5个数的和必须相同。例如：图2中，把相差为1的九个数（1至9）填入后，三个“边区域”及“核心区域”的数的和都是22，即6+1+9+2+4=22，4+2+8+3+5=22，5+3+7+1+6=22，2+9+1+7+3=22
（1）操作与发现：
在图3中，小明把差为1的连续九个正整数（1至9）分为三组，其中1、2、3为同一组，4、5、6为同一组，7、8、9为同一组，把同组数填进同一花纹的△中，生成了一个符合定义的魔法三角阵，且各区域的5个数的和为28，请你在图3中把小明的发现填写完整.
（2）操作与应用：
根据（1）发现的结果，把差为8的连续九个正整数填进图4中，仍能得到符合定义的魔法三角阵，且各区域的5个数的和为2019.
①设其中最小的数为
，则最大的数是_________;（用含的式子表示）.
②把图4中的9个数填写完整，并说明理由.
【答案】（1）答案见解析；（2）①
；②答案见解析，理由见解析.
【解析】
（1）首先确定三角形顶点的三个数，再进一步间隔确定，再做局部调整即可解答；
（2）①根据题意具体表示出前几个数字，然后推广到一般情形，发现规律解决问题；
②根据（1）的提示，可设这9个数为：
，，再根据（1）填出的数据，可以顺序填上对应的位置，按照核心区域相加得2019列出方程，解得对应的数.
（1）
或
或
（2）①解：由题意可知，连续九个正整数的差为8，
设其中最小的数为
，
则第二个数为
，
第三个数为
…
以此类推，
第九个数为
，
所以最大数是.
②
理由：根据（1）的提示，可设这9个数为： ，，按照核心区域相加得2019可以列出方程：
，解得：
，
所以这9个数为：367，375，383，391，399，407，415，423，431.
