题目内容
(2013•尤溪县质检)如图所示,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是

①
①
(填序号)
分析:通过设出BE=x,FC=y,且△AEF为直角三角形,运用勾股定理得出y与x的关系,在判断出函数图象.
解答:解:设BE=x,FC=y,则AE2=x2+42,EF2=(4-x)2+y2,AF2=(4-y)2+42.
又∵△AEF为直角三角形,
∴根据勾股定理得到AE2+EF2=AF2.即x2+42+(4-x)2+y2=(4-y)2+42
化简得:y=-
x2+x=-
(x-2)2+1,即y=(x-2)2+1,
此时,该函数图象是以(2,1)为顶点的抛物线.
很明显,y关于x的函数图象是①.
故填:①.
又∵△AEF为直角三角形,
∴根据勾股定理得到AE2+EF2=AF2.即x2+42+(4-x)2+y2=(4-y)2+42
化简得:y=-
| 1 |
| 4 |
| 1 |
| 4 |
此时,该函数图象是以(2,1)为顶点的抛物线.
很明显,y关于x的函数图象是①.
故填:①.
点评:本题考查了动点问题的函数图象,解题的关键是列出动点的函数关系式,根据函数关系式来判定其函数图象.

练习册系列答案
相关题目
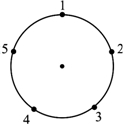 (2013•尤溪县质检)如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下次沿顺时针方向跳两个点;若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2013次后它停在哪个数对应的点上( )
(2013•尤溪县质检)如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下次沿顺时针方向跳两个点;若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2013次后它停在哪个数对应的点上( )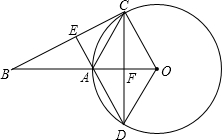 (2013•尤溪县质检)如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.
(2013•尤溪县质检)如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.