题目内容
如图是一张直角三角形的纸片，两直角边AC＝6 cm、BC＝8 cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为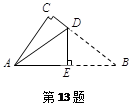 
5
答案为：15/4cm
在RT△ABC中，可求出AB的长度，根据折叠的性质可得出AE=EB=1/2 AB，在RT△ADE中，利用tanB=tan∠DAE即可得出DE的长度．
解：∵AC=6cm，BC=8cm，
∴AB=
=10cm，tanB=3/4，
由折叠的性质得，∠B=∠DAE，tanB=tan∠DAE=3/4，
AE=EB=1/2AB=5cm，
∴DE=AEtan∠DAE=15/4cm．
故答案为：15/4cm．
在RT△ABC中，可求出AB的长度，根据折叠的性质可得出AE=EB=1/2 AB，在RT△ADE中，利用tanB=tan∠DAE即可得出DE的长度．
解：∵AC=6cm，BC=8cm，
∴AB=
=10cm，tanB=3/4，由折叠的性质得，∠B=∠DAE，tanB=tan∠DAE=3/4，
AE=EB=1/2AB=5cm，
∴DE=AEtan∠DAE=15/4cm．
故答案为：15/4cm．
练习册系列答案
相关题目
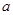m，宽为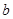
m的一块草坪上修了一条1m宽的笔直小路，则余下草坪的面积可表示为__________m2，现为增加美感，把这条小路改为竖直方向的宽恒为1m的弯曲小路，则此时余下草坪的面积为__________ m2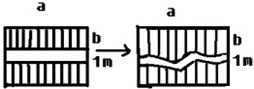
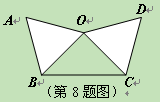
经过旋转得到的．如果用有序数对(2,1)表示方格纸上A点的位置，用(1,2)表示B点的位置，那么四边形
