题目内容
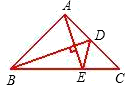 如图Rt△ABC中,∠BAC=90°,AB=AC,D为AC的中点,AE⊥BD交BC于E,若∠BDE=a,∠ADB的大小是
如图Rt△ABC中,∠BAC=90°,AB=AC,D为AC的中点,AE⊥BD交BC于E,若∠BDE=a,∠ADB的大小是
- A.a
- B.90°-a
- C.
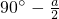
- D.
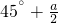
C
分析:可作AM⊥BC于M,交BD与G,求解△AGB≌△CEA与△ADG≌△CDE,进而通过角之间的转化,最终可得出结论.
解答:如图,作AM⊥BC于M,AM交BD于G,
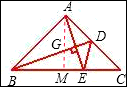
在△AGB和△CEA中,∠GAB=∠ECA=45°,AB=AC,∠AGB=90°+∠GBM=∠AEC.
∴△AGB≌△CEA,
∴AG=CE.又AD=CD,∠DAG=∠DCE,
∴△ADG≌△CDE.
∴∠ADG=∠CDE,
∴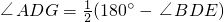 ,
,
= .
.
故选C.
点评:本题主要考查了全等三角形的判定及性质以及三角形内角和定理,能够运用其性质求解一些简单的计算问题.
分析:可作AM⊥BC于M,交BD与G,求解△AGB≌△CEA与△ADG≌△CDE,进而通过角之间的转化,最终可得出结论.
解答:如图,作AM⊥BC于M,AM交BD于G,

在△AGB和△CEA中,∠GAB=∠ECA=45°,AB=AC,∠AGB=90°+∠GBM=∠AEC.
∴△AGB≌△CEA,
∴AG=CE.又AD=CD,∠DAG=∠DCE,
∴△ADG≌△CDE.
∴∠ADG=∠CDE,
∴
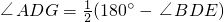 ,
,=
 .
.故选C.
点评:本题主要考查了全等三角形的判定及性质以及三角形内角和定理,能够运用其性质求解一些简单的计算问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
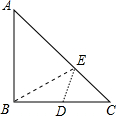 如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )
如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
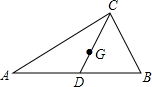 如图Rt△ABC中,∠C=90°,AC=8,BC=6,CD为AB边上的中线,点G是重心,则DG=
如图Rt△ABC中,∠C=90°,AC=8,BC=6,CD为AB边上的中线,点G是重心,则DG= 如图Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从B出发,以1cm/s的速度向C运动,同时点Q从C出发,以1cm/s的速度向A运动,问几秒时PQ的长为2
如图Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从B出发,以1cm/s的速度向C运动,同时点Q从C出发,以1cm/s的速度向A运动,问几秒时PQ的长为2
 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.