题目内容
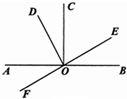 16、如图,直线AB、EF交于点O.已知 CO⊥AB,∠DOE=90°.有以下四个结论:
16、如图,直线AB、EF交于点O.已知 CO⊥AB,∠DOE=90°.有以下四个结论:①∠AOF=∠DOC ②∠AOE=∠BOD ③∠AOD=∠COE ④∠COF=∠DOB,其中正确结论的序号是
①③④
.(注:错选得0分,少选则按选对一个得1分计.)分析:根据题意和图形对四个答案依次分析即可.
解答:解:①∵CO⊥AB,∠DOE=90°,
∴∠BOE+∠COE=90°,∠DOC+∠COE=90°,
又∵∠COE=∠COE,
∴∠BOE=∠DOC,
又∵∠AOF=∠BOE(对顶角相等),
∴∠AOF=∠∠DOC,故①正确;
②∠AOE=180°-∠BOE,∠BOD=180°-∠AOD,
∵∠AOD≠∠BOE,
∴∠AOE≠∠BOD,故②错误;
③∵∠AOC=∠AOD+∠DOC=90°,∠BOC=∠COE+∠BOE,
又∵∠BOE=∠DOC,
∴∠AOD=∠COE,故③正确;
④∵∠COF=90°+∠AOF,∠DOB=90°+∠DOC,
又∵∠AOF=∠DOC,
∴∠COF=∠DOB,故④正确.
故答案为:①③④.
∴∠BOE+∠COE=90°,∠DOC+∠COE=90°,
又∵∠COE=∠COE,
∴∠BOE=∠DOC,
又∵∠AOF=∠BOE(对顶角相等),
∴∠AOF=∠∠DOC,故①正确;
②∠AOE=180°-∠BOE,∠BOD=180°-∠AOD,
∵∠AOD≠∠BOE,
∴∠AOE≠∠BOD,故②错误;
③∵∠AOC=∠AOD+∠DOC=90°,∠BOC=∠COE+∠BOE,
又∵∠BOE=∠DOC,
∴∠AOD=∠COE,故③正确;
④∵∠COF=90°+∠AOF,∠DOB=90°+∠DOC,
又∵∠AOF=∠DOC,
∴∠COF=∠DOB,故④正确.
故答案为:①③④.
点评:本题考查了角的计算,解题用到了垂直、对顶角的知识,解题的关键是图形结合.

练习册系列答案
相关题目
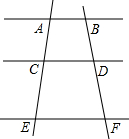 如图,直线AB∥CD∥EF,若AC=3,CE=4,则
如图,直线AB∥CD∥EF,若AC=3,CE=4,则| BD |
| BF |
A、
| ||
B、
| ||
C、
| ||
D、
|
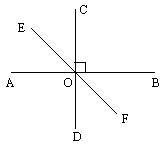 16、如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=128°19′,则∠BOF,∠AOF的度数分别为
16、如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=128°19′,则∠BOF,∠AOF的度数分别为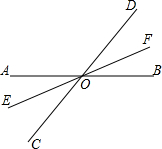 如图,直线AB,EF相交于点O,∠AOE=30°,∠BOC=2∠AOC,求∠DOF的度数.
如图,直线AB,EF相交于点O,∠AOE=30°,∠BOC=2∠AOC,求∠DOF的度数.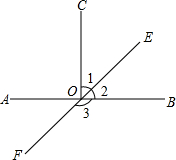 如图,直线AB和EF相交于O,OC平分∠AOB,∠1=65°,试求∠3的度数.
如图,直线AB和EF相交于O,OC平分∠AOB,∠1=65°,试求∠3的度数.