题目内容
【题目】问题发现:
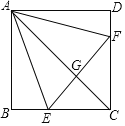
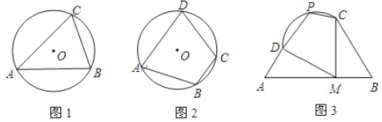
(1)如图1,![]() 内接于半径为4的
内接于半径为4的![]() ,若
,若![]() ,则
,则![]() _______;
_______;
问题探究:
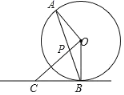
(2)如图2,四边形![]() 内接于半径为6的
内接于半径为6的![]() ,若
,若![]() ,求四边形
,求四边形![]() 的面积最大值;
的面积最大值;
解决问题
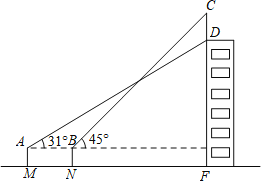
(3)如图3,一块空地由三条直路(线段![]() 、AB、
、AB、![]() )和一条弧形道路
)和一条弧形道路![]() 围成,点
围成,点![]() 是
是![]() 道路上的一个地铁站口,已知
道路上的一个地铁站口,已知![]()
![]() 千米,
千米,![]() 千米,
千米,![]() ,
,![]() 的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点
的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点![]() 处,另外三个入口分别在点
处,另外三个入口分别在点![]() 、
、![]() 、
、![]() 处,其中点
处,其中点![]() 在
在![]() 上,并在公园中修四条慢跑道,即图中的线段
上,并在公园中修四条慢跑道,即图中的线段![]() 、
、![]() 、
、![]() 、
、![]() ,是否存在一种规划方案,使得四条慢跑道总长度(即四边形
,是否存在一种规划方案,使得四条慢跑道总长度(即四边形![]() 的周长)最大?若存在,求其最大值;若不存在,说明理由.
的周长)最大?若存在,求其最大值;若不存在,说明理由.
【答案】(1)![]() ;(2)四边形ABCD的面积最大值是
;(2)四边形ABCD的面积最大值是![]() ;(3)存在,其最大值为
;(3)存在,其最大值为![]() .
.
【解析】
(1)连接OA、OB,作OH⊥AB于H,利用![]() 求出∠AOH=
求出∠AOH=![]() ∠AOB=
∠AOB=![]() ,根据OA=4,利用余弦公式求出AH,即可得到AB的长;
,根据OA=4,利用余弦公式求出AH,即可得到AB的长;
(2)连接AC,由![]() 得出AC=
得出AC=![]() ,再根据四边形
,再根据四边形![]() 的面积=
的面积= ![]() ,当DH+BM最大时,四边形ABCD的面积最大,得到BD是直径,再将AC、BD的值代入求出四边形面积的最大值即可;
,当DH+BM最大时,四边形ABCD的面积最大,得到BD是直径,再将AC、BD的值代入求出四边形面积的最大值即可;
(3)先证明△ADM≌△BMC,得到△CDM是等边三角形,求得等边三角形的边长CD,再根据完全平方公式的关系得出PD=PC时PD+PC最大,根据CD、∠DPC求出PD,即可得到四边形周长的最大值.
(1)连接OA、OB,作OH⊥AB于H,
∵![]() ,
,
∴∠AOB=120![]() .
.
∵OH⊥AB,
∴∠AOH=![]() ∠AOB=
∠AOB=![]() ,AH=BH=
,AH=BH=![]() AB,
AB,
∵OA=4,
∴AH=![]() ,
,
∴AB=2AH=![]() .
.
故答案为:![]() .
.
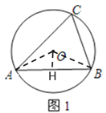
(2)∵∠ABC=120![]() ,四边形ABCD内接于
,四边形ABCD内接于![]() ,
,
∴∠ADC=60![]() ,
,
∵![]() 的半径为6,
的半径为6,
∴由(1)得AC=![]() ,
,
如图,连接AC,作DH⊥AC,BM⊥AC,
∴四边形![]() 的面积=
的面积= ![]() ,
,
当DH+BM最大时,四边形ABCD的面积最大,连接BD,则BD是![]() 的直径,
的直径,
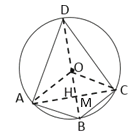
∴BD=2OA=12,BD⊥AC,
∴四边形![]() 的面积=
的面积=![]() .
.
∴四边形ABCD的面积最大值是![]()
(3)存在;
∵![]()
![]() 千米,
千米,![]() 千米,
千米,![]() ,
,
∴△ADM≌△BMC,
∴DM=MC,∠AMD=∠BCM,
∵∠BCM+∠BMC=180![]() -∠B=120
-∠B=120![]() ,
,
∴∠AMD+∠BMC=120![]() ,
,
∴∠DMC=60![]() ,
,
∴△CDM是等边三角形,
∴C、D、M三点共圆,
∵点P在弧CD上,
∴C、D、M、P四点共圆,
∴∠DPC=180![]() -∠DMC=120
-∠DMC=120![]() ,
,
∵![]() 弧的半径为1千米,∠DMC=60
弧的半径为1千米,∠DMC=60![]() ,
,
∴CD=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当PD=PC时,PD+PC最大,此时点P在弧CD的中点,交DC于H ,
在Rt△DPH中,∠DHP=90![]() ,∠DPH=60
,∠DPH=60![]() ,DH=
,DH=![]() DC=
DC=![]() ,
,
∴![]() ,
,
∴四边形![]() 的周长最大值=DM+CM+DP+CP=
的周长最大值=DM+CM+DP+CP=![]() .
.

 阅读快车系列答案
阅读快车系列答案