题目内容
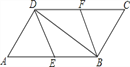
【题目】如图,在□ABCD中,点E,F分别是边AB,CD的中点,(1)求证:△CFB≌△AED;
(2)若∠ADB=90°,判断四边形BFDE的形状,并说明理由;
【答案】(1)见解析;(2) 四边形BFDE是菱形.
【解析】分析:(1)首先根据平行四边形的性质,得到相等的边角和平行线,然后根据中点的性质和全等三角形的判定SAS证明即可;
(2)连接EF,根据一组对边平行且相等的四边形是平行四边形证得:四边形四边形![]() 是平行四边形,四边形
是平行四边形,四边形![]() 是平行四边形,然后根据平行线的性质证明,最后得到对角线互相垂直的平行四边形是菱形.
是平行四边形,然后根据平行线的性质证明,最后得到对角线互相垂直的平行四边形是菱形.
详解:(1)证明:![]() 四边形
四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]() ,
,![]()
又∵点E,F分别是AB,CD的中点
∴![]()
∴![]()
(2)解法一:四边形![]() 是菱形。证明如下:
是菱形。证明如下:
连接EF
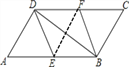
∵四边形![]() 是平行四边形
是平行四边形
∴![]()
又∵点E,F分别是AB,CD的中点
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
同理,四边形![]() 是平行四边形
是平行四边形
∴![]()
∴![]()
∴![]()
∴四边形![]() 是菱形。
是菱形。

(2)解法二:四边形![]() 是菱形。证明如下:
是菱形。证明如下:
∵四边形![]() 是平行四边形
是平行四边形
∴![]()
又∵点E,F分别是AB,CD的中点
∴![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
又∵![]()
∴在![]() 中,
中,![]()
∴四边形![]() 是菱形。
是菱形。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目