Question

【题目】如图，将矩形ABCO放在直角坐标系中，其中顶点B的坐标为（10，8），E是BC边上一点，将△ABE沿AE折叠，点B刚好与OC边上点D重合，过点E的反比例函数y= 的图象与边AB交于点F，则线段AF的长为（ ）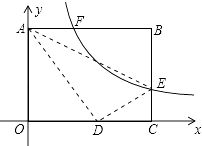
A.
B.2
C.
D.

Answer 1

【答案】A
【解析】解：∵△ABE沿AE折叠，点B刚好与OC边上点D重合， ∴AD=AB=10，DE=BE，
∵AO=8，AD=10，
∴OD= ，CD=10﹣6=4，
设点E的坐标是（10，b），
则CE=b，DE=10﹣b，
∵CD2+CE2=DE2 ，
∴42+b2=（8﹣b）2 ，
解得b=3，
∴点E的坐标是（10，3），
∴k=10×3=30，
∴线段AF的长为：30 ．
故选：A．
【考点精析】关于本题考查的翻折变换（折叠问题），需要了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．