题目内容
【题目】如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证: 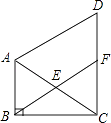
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.
【答案】
(1)证明:∵△ACD是等边三角形,
∴∠DCA=60°,
∵∠BAC=60°,
∴∠DCA=∠BAC,
在△ABE与△CFE中,
 ,
,
∴△ABE≌△CFE
(2)证明:∵E是AC的中点,
∴BE=EA,
∵∠BAE=60°,
∴△ABE是等边三角形,
∴△CEF是等边三角形,
∴∠CFE=60°,
∵△ACD是等边三角形,
∴∠CDA=∠DCA=60°,
∴∠CFE=∠CDA,
∴BF∥AD,
∵∠DCA=∠BAC=60°,
∴AB∥DC,
∴四边形ABFD是平行四边形
【解析】(1)根据等边三角形的性质得到∠DCA=60°等量代换得到∠DCA=∠BAC,根据全等三角形的判定定理即可得到结论;(2)根据已知条件得到△ABE是等边三角形,推出△CEF是等边三角形,证得∠CFE=∠CDA,求得BF∥AD,即可得到结论;本题考查了平行四边形的判定,全等三角形的判定和性质,等边三角形的判定和性质,熟练熟练掌握平行四边形的判定定理是解题的关键.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握平行四边形的判定(两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形)的相关知识才是答题的关键.

练习册系列答案
相关题目