题目内容
【题目】如图，△ABC 中，点 D,E 分别在∠ABC 和∠ACB 的平分线上，连接 BD,DE,EC,若∠D+∠E=295°， 则∠A 是（ ）
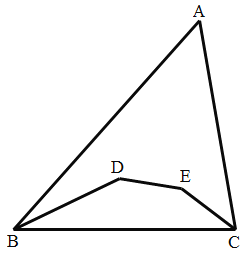
A.65°B.60°C.55°D.50°
【答案】D
【解析】
利用四边形BDEC的内角和为360°，即可求出∠DBC+∠ECB的度数，由BD、CE分别平分∠ABC、∠ACB可得∠ABC=2∠DBC, ∠ACB=2∠ECB，可求∠ABC+∠ACB
的度数，即可得∠A的度数.
解：在四边形BDEC中，∠DBC+∠EBC+∠D+∠E=360°
∵∠D+∠E=295°
∴∠DBC+∠ECB =360°-295°=65°
∵BD、CE分别平分∠ABC、∠ACB
∴∠ABC=2∠DBC, ∠ACB=2∠ECB
∴∠ABC+∠ACB=2∠DBC+2∠ECB=2(∠DBC+∠ECB)=130°
∴∠A=50°
故选：D
练习册系列答案
相关题目
【题目】某弹簧挂上不超过20千克的物体后按一定规律伸长，测得一弹簧的长度
（厘米）与所挂的物体的质量
（千克）有下面的关系：
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
那么弹簧的总长（厘米）与所挂的物体的质量（千克）之间是否是函数关系？若是，请写出函数关系式.
