题目内容
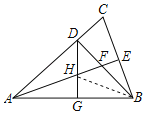
【题目】如图,在△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于点F交BC于点E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
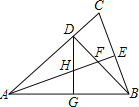
A.AH=2DFB.HE=BEC.AF=2CED.DH=DF
【答案】A
【解析】
通过证明△ADF≌△BDC,可得AF=BC=2CE,由等腰直角三角形的性质可得AG=BG,DG⊥AB,由余角的性质可得∠DFA=∠AHG=∠DHF,可得DH=DF,由线段垂直平分线的性质可得AH=BH,可求∠EHB=∠EBH=45°,可得HE=BE,即可求解.
解:∵∠BAC=45°,BD⊥AC,
∴∠CAB=∠ABD=45°,
∴AD=BD,
∵AB=AC,AE平分∠BAC,
∴CE=BE=![]() BC,∠CAE=∠BAE=22.5°,AE⊥BC,
BC,∠CAE=∠BAE=22.5°,AE⊥BC,
∴∠C+∠CAE=90°,且∠C+∠DBC=90°,
∴∠CAE=∠DBC,且AD=BD,∠ADF=∠BDC=90°,
∴△ADF≌△BDC(AAS)
∴AF=BC=2CE,故选项C不符合题意,
∵点G为AB的中点,AD=BD,∠ADB=90°,∠CAE=∠BAE=22.5°,
∴AG=BG,DG⊥AB,∠AFD=67.5°
∴∠AHG=67.5°,
∴∠DFA=∠AHG=∠DHF,
∴DH=DF,故选项D不符合题意,
连接BH,
∵AG=BG,DG⊥AB,
∴AH=BH,
∴∠HAB=∠HBA=22.5°,
∴∠EHB=45°,且AE⊥BC,
∴∠EHB=∠EBH=45°,
∴HE=BE,
故选项B不符合题意,
故选:A.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目